Question

The equation of the circle which touches the axis of y at a distance of 4 from the origin and cuts the intercepts of 6 units from the axis of x is
(a) ${{x}^{2}}+{{y}^{2}}\pm 10x\pm 8y+16=0$
(b) ${{x}^{2}}+{{y}^{2}}\pm 5x\pm 4y+16=0$
(c) ${{x}^{2}}+{{y}^{2}}\pm 10x\pm 8y-16=0$
(d) ${{x}^{2}}+{{y}^{2}}\pm 5x\pm 4y-16=0$

Answer 1

We will take the help of the diagram here. Then we will use the Pythagoras theorem here by which we will find the radius of the circle. Then we will use the formula of the equation of the circle as ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$ where r is the radius of the circle and the points $\left( {{x}_{1}},{{y}_{1}} \right)$ is the centre of the circle. Then, we will apply algebraic formulas ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ and ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ for the expansion of the equation of the circle after substituting the radius r.

Complete step-by-step answer:
First we will draw a figure according to the question. The required diagram is shown below.

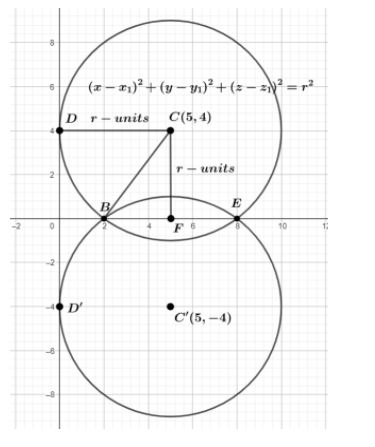
Now, by looking at the figure we will focus on the circle which is with centre C. Here the radiuses are CD and CB represented as r units ( we can take it as units ). CF is perpendicular on BE. We can clearly notice that the circle touches the axis of y at a distance of 4 from the origin therefore, CF = 4 units, and cuts the intercepts of 6 units from the axis of x thus we get that BE is 6 units. Thus, CF divides BE into BF and FE. Therefore, we get BE = 2 BF or BF = $\dfrac{BE}{2}$ which results in $\dfrac{6}{2}$ or 3 units. So, BF and FE are both 3 units. Now we will consider the triangle $\Delta CBF$ and apply the Pythagoras theorem to it. Thus we will get
$\begin{aligned} & C{{B}^{2}}=B{{F}^{2}}+C{{F}^{2}} \\\ & \Rightarrow {{r}^{2}}={{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}} \\\ & \Rightarrow {{r}^{2}}=9+16 \\\ & \Rightarrow {{r}^{2}}=25 \\\ & \Rightarrow r=\pm 5 \\\ \end{aligned}$
Now we have the radius as a positive number therefore, we will have CB as 5 cm. This is the radius of the circle. Now we will apply the equation of the circle as ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$ where r is the radius of the circle and the points $\left( {{x}_{1}},{{y}_{1}} \right)$ is the centre of the circle. So, by substituting r = 5 units and the point $\left( 5,4 \right)$ therefore we will get
$\begin{aligned} & {{\left( x-5 \right)}^{2}}+{{\left( y-4 \right)}^{2}}={{\left( 5 \right)}^{2}} \\\ & \Rightarrow {{\left( x-5 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=25 \\\ \end{aligned}$
Now, we will use the formula ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ therefore, we get
$\begin{aligned} & \Rightarrow {{x}^{2}}+{{\left( 5 \right)}^{2}}-2\left( 5 \right)x+{{y}^{2}}+{{\left( 4 \right)}^{2}}-2\left( 4 \right)y=25 \\\ & \Rightarrow {{x}^{2}}+25-10x+{{y}^{2}}+16-8y=25 \\\ & \Rightarrow {{x}^{2}}-10x+{{y}^{2}}+16-8y=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-10x-8y+16=0 \\\ \end{aligned}$
Similarly if we consider the circle with the point $\left( -5,-4 \right)$ then, we will get the answer as
$\begin{aligned} & {{\left( x-\left( -5 \right) \right)}^{2}}+{{\left( y-\left( -4 \right) \right)}^{2}}={{\left( 5 \right)}^{2}} \\\ & \Rightarrow {{\left( x+5 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=25 \\\ \end{aligned}$
Now, we will use the formula ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ therefore, we get
$\begin{aligned} & \Rightarrow {{x}^{2}}+{{\left( 5 \right)}^{2}}+2\left( 5 \right)x+{{y}^{2}}+{{\left( 4 \right)}^{2}}+2\left( 4 \right)y=25 \\\ & \Rightarrow {{x}^{2}}+25+10x+{{y}^{2}}+16+8y=25 \\\ & \Rightarrow {{x}^{2}}+10x+{{y}^{2}}+16+8y=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+10x-8y+16=0 \\\ \end{aligned}$
Therefore, the equation is ${{x}^{2}}+{{y}^{2}}\pm 10x\pm 8y+16=0$.

So, the correct answer is “Option A”.

Note: There is a need of considering two points here. This is because we are supposed to find the equation which is actually the 2 different equations merged together in the end. The diagram is most important here. If we will not draw the right diagram then we will get the radius wrong as well as the equation of the circle wrong. So, to get to the right answer one should draw the diagram properly. One should notice that the equation of the circle here is touching the axis of y at a distance of 4 from the origin and cuts the intercepts of 6 units from the axis of x. In case we have y as x and x as y hen we will draw a different diagram.