Question
Question: The equation of the circle passing through the foci of the ellipse \(\dfrac{{{x^2}}}{{16}} + \dfrac{...
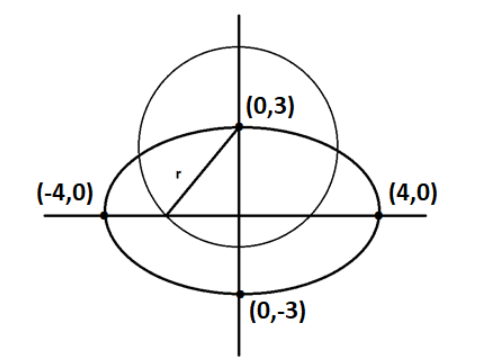
The equation of the circle passing through the foci of the ellipse 16x2+9y2=1, and having centre at (0,3) is
A. x2+y2−6y+7=0
B. x2+y2−6y−5=0
C. x2+y2−6y+5=0
D. x2+y2−6y−7=0
Solution
To solve this question, we should remember the basic points of the standard equation of circle and as well as ellipse. The foci of the ellipse will be (±ae,0) where a is the x coordinate of the ellipse and e is the eccentricity. The distance between the foci and the centre of the circle will be the radius of that circle.
Complete step-by-step answer :
Given that,
Equation of ellipse = 16x2+9y2=1 ………… (i)
Centre of circle = (0,3)
The standard equation of ellipse is given by,
⇒a2x2+b2y2=1
Comparing this with equation (i), we will get
a = 4 and b = 3.
Here, we can see that a > b,
So, the foci of the ellipse will be (±ae,0)
We know that,
Eccentricity, e=1−a2b2
Putting values of a and b, we will get
Therefore,
Foci = (±7,0)
As according to the question, the circle is passing through the foci of the ellipse, i.e. (±7,0) and we have already given the centre of the circle as (0,3).
Therefore,
Radius of circle = distance between (7,0) and (0,3).
Radius, r = (7−0)2+(0−3)2
r = 7+9=16
r = 4.
We know that, the general equation of a circle is given by,
⇒(x−h)2+(y−k)2=r2, where (h,k) is the centre of the circle.
Putting all the values here, we will get
Hence, the required equation of the circle is x2+y2−6y−7=0.
Therefore, the correct answer is option (A).
Note : Whenever we ask such type of questions, first, we have to know some basic points of the ellipse. The eccentricity of an ellipse is also given by, ac and c=a2−b2. When c = 0, both foci merge together with the centre of the ellipse and a2=b2, i.e. a = b, and so the ellipse becomes a circle.
