Question

The equation of motion of a compound pendulum is
A. $\dfrac{{{d^2}x}}{{d{t^2}}} + {\omega ^2}x = 0$
B. $\dfrac{{{d^2}\theta }}{{d{t^2}}} + {\omega ^2}\theta = 0$
C. $F = - kx$
D. $\dfrac{{d\theta }}{{d{t^2}}} + {\omega ^2}\theta = 0$

Answer 1

A compound pendulum is basically a rigid body allowed to oscillate about a horizontal axis passing through it. So the compound pendulum is almost a simple pendulum but has an angular displacement associated with it. Derive the equation of compound pendulum using necessary conditions for SHM and compare with the options for the right answer.

Complete step-by-step answer:
The conditions of an ideal pendulum cannot be realized in actual practice. So a compound pendulum is used to get rid of most defects caused by the simple pendulum. A compound pendulum consists of a rigid body that can oscillate freely about a horizontal axis passing through it.
Consider a rigid body of any shape and mass m capable of oscillating freely about a horizontal axis passing through it perpendicular to the plane.
Let O be the center of suspension of the body and G its center of gravity vertically below O at a distance l in the position of rest. When the body is displaced through a small angle $\theta$ to the dotted position, the center of gravity is shifted to position G’ and its weight mg acts vertically downwards at G’.

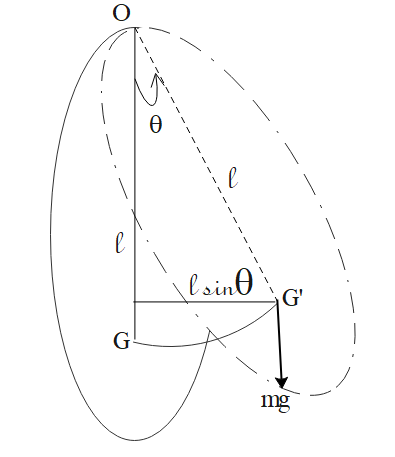
If the pendulum is now released a restoring couple acts on it and brings it back to its initial position. But due to inertia, it overshoots the mark and hence starts oscillating about the mean position.
The moment of the restoring couple or Torque,
$\tau = - mg \times G'A = - mgl\sin \theta \approx - mgl\theta \cdots \cdots \cdots \left( 1 \right)$
Since the angle $\theta$ through which the pendulum is displaced is small so that$\sin \theta \approx \theta$.
This restoring couple gives rise to an angular acceleration$\alpha$ in the pendulum. If $I$is the moment of inertia of the rigid body about aan axis passing through its center of suspension, then restoring couple is given by:
$\tau = I\alpha = I\dfrac{{{d^2}\theta }}{{d{t^2}}} \cdots \cdots \cdots \cdots \left( 2 \right)$
Comparing equation (1) and (2), we get:
\eqalign{ & I\dfrac{{{d^2}\theta }}{{d{t^2}}} = - mgl\theta \cr & {\text{or }}\dfrac{{{d^2}\theta }}{{d{t^2}}} = - \dfrac{{mgl}}{I}\theta \cr & \Rightarrow \dfrac{{{d^2}\theta }}{{d{t^2}}} \propto \theta \cr}
Clearly, the equation of a compound pendulum is a second order derivative of angular displacement$\theta$.
Therefore, the correct option is B i.e., $\dfrac{{{d^2}\theta }}{{d{t^2}}} + {\omega ^2}\theta = 0$
Note: The center of suspension and center of oscillation of a compound pendulum is interchangeable in nature for a compound pendulum. This can be practically proved using a Kater’s pendulum, which is also known as a reversible pendulum.