Question

The equation of line with slope 3 and passing through (1, 3) is

Answer 1

Hint : Given the linear equation of line passes through one point (1, 3) and has a slope 3. The linear equation when one point and slope is given is $y - {y_1} = m\left( {x - {x_1}} \right)$ , where (x1, y1) is the given point and m is the slope. Use this line equation form to find the line equation. Substitute the known values in this equation to find the line equation.

Complete step-by-step answer :
We are given that the equation of a line with slope 3 passes through a point (1, 3).
We have to find the line equation using $y - {y_1} = m\left( {x - {x_1}} \right)$
The line equation will be
$y - {y_1} = m\left( {x - {x_1}} \right) \\\ m = 3,\left( {{x_1},{y_1}} \right) = \left( {1,3} \right) \\\ y - 3 = 3\left( {x - 1} \right) \\\ y - 3 = 3x - 3 \\\$
Send 3x to the left hand side and -3 to the right hand side, then the above equation becomes
$3x - y = 3 - 3 \\\ 3x - y = 0 \\\ 3x = y \\\ y = 3x \\\$

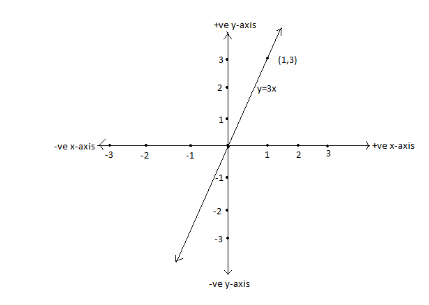
Therefore, the equation of line with slope 3 passes through (1, 3) is $y = 3x$

Note : Linear equations in two variables will have maximum two variables and will have the highest degree as 1 for both the variables. There are many ways to find the equation of a line in two variables. We used slope point form in the above solution. Other forms are slope-intercept form where a slope and y-intercept will be given; intercept form where x-intercept and y-intercept will be given; two points form where two points in which line passes through them will be given and standard form.