Question

The equation of common tangent to the parabola ${y^2} = 4ax{\text{ and }}{x^2} = 4by$ is
${\text{A}}{\text{. }}x{a^{\dfrac{1}{3}}} + y{b^{\dfrac{1}{3}}} + {(ab)^{\dfrac{2}{3}}} = 0 \\\ {\text{B}}{\text{. }}\dfrac{1}{{{a^{\dfrac{1}{3}}}}} + \dfrac{y}{{{b^{\dfrac{1}{3}}}}} + \dfrac{1}{{{{(ab)}^{\dfrac{2}{3}}}}} = 0 \\\ {\text{C}}{\text{. }}y{a^{\dfrac{1}{3}}} + x{b^{\dfrac{1}{3}}} - {(ab)^{\dfrac{2}{3}}} = 0 \\\ {\text{D}}{\text{. }}\dfrac{1}{{{b^{\dfrac{1}{3}}}}} + \dfrac{y}{{{a^{\dfrac{1}{3}}}}} - \dfrac{1}{{{{(ab)}^{\dfrac{2}{3}}}}} = 0 \\\$

Answer 1

Hint: In this question ${y^2} = 4ax$ is a parabola whose axis is x-axis and ${x^2} = 4by$ is also a parabola whose axis is y-axis. We have to write their respective equations of tangents. Since, it is given that tangents are common, use the equation in a slope so we can equate slopes and y-intercept of both parabolas to get an equation of common tangent to both.

Complete step-by-step answer:

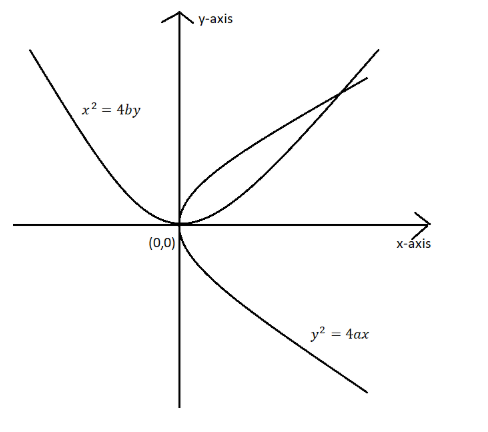
We know equation of tangent to parabola to ${y^2} = 4ax$ is given by
$\Rightarrow y = mx + \dfrac{a}{m}{\text{ \\{ }}m{\text{ is the slope of tangent\\} eq}}{\text{.1}}$
And the equation of tangent to parabola to ${x^2} = 4by$ is given by
$\Rightarrow x = {m_1}y + \dfrac{a}{{{m_1}}}{\text{ \\{ }}{m_1} = {\text{slope of tangent\\} }} \\\ \Rightarrow y = \dfrac{1}{{{m_1}}}x + \dfrac{a}{{{{({m_1})}^2}}}{\text{ eq}}{\text{.2}} \\\$
For common tangent, eq.1 and eq.2 represent the same line. Therefore, the same slope and the same y-intercept.
$\therefore m = \dfrac{1}{{{m_1}}}{\text{ eq}}{\text{.3}} \\\ {\text{and }}\dfrac{a}{m} = - \dfrac{b}{{{m_1}^2}}{\text{ eq}}{\text{.4}} \\\$
Now considering eq.4 using relation of eq.3, we get
$\Rightarrow \dfrac{a}{m} = - \dfrac{b}{{{{({m_1})}^2}}} \\\ \Rightarrow \dfrac{a}{m} = - b{m^2} \\\ \Rightarrow a = - b{m^3} \\\ \Rightarrow m = {\left( {\dfrac{{ - a}}{b}} \right)^{\dfrac{1}{3}}}{\text{ eq}}{\text{.5}} \\\$
Now, put value of$m$from eq.5 into eq.1 we get the equation of common tangent to both the given parabola
$\Rightarrow y = mx + \dfrac{a}{m} \\\ \Rightarrow y = mx + \dfrac{a}{m} \\\ \Rightarrow y = {\left( {\dfrac{{ - a}}{b}} \right)^{\dfrac{1}{3}}}x + \dfrac{a}{{{{\left( {\dfrac{{ - a}}{b}} \right)}^{\dfrac{1}{3}}}}}{\text{ \\{ }}m = {\left( {\dfrac{{ - a}}{b}} \right)^{\dfrac{1}{3}}}\\} \\\ \Rightarrow y = {\left( {\dfrac{{ - a}}{b}} \right)^{\dfrac{1}{3}}}x + a{\left( {\dfrac{{ - b}}{a}} \right)^{\dfrac{1}{3}}} \\\$
Now on rearranging the terms of above equation to get answer in form of given options
Using property$\Rightarrow \dfrac{{{a^m}}}{{{a^n}}} = {a^{m - n}}$
We can rewrite above equation as

\Rightarrow y = {\left( {\dfrac{{ - a}}{b}} \right)^{\dfrac{1}{3}}}x + {(a)^{\dfrac{2}{3}}}{\left( { - b} \right)^{\dfrac{1}{3}}} \\\ \Rightarrow {(b)^{\dfrac{1}{3}}}y = {\left( { - a} \right)^{\dfrac{1}{3}}}x + {(a)^{\dfrac{2}{3}}}{\left( { - b} \right)^{\dfrac{1}{3}}}{(b)^{\dfrac{1}{3}}} \\\

Now using property${a^m}.{a^n} = {a^{m + n}}$, we can write above equation as

\Rightarrow {\left( a \right)^{\dfrac{1}{3}}}x + {(b)^{\dfrac{1}{3}}}y + {(a)^{\dfrac{2}{3}}}{(b)^{\dfrac{2}{3}}} = 0 \\\ \Rightarrow {\left( a \right)^{\dfrac{1}{3}}}x + {(b)^{\dfrac{1}{3}}}y + {(ab)^{\dfrac{2}{3}}} = 0 \\\

Hence, option A. is correct.

Note: Whenever you get this type of question the key concept to solve this is to learn equation of tangents of different curves in different conditions like in this question we require tangent of parabola in different scenario($y = mx + \dfrac{a}{m}$ and $x = {m_1}y + \dfrac{a}{{{m_1}}}{\text{ }}$).