Question

The equation of a straight line which passes through the point $\left( 1,-2 \right)$ and cuts off equal intercept from axes will be:
(a) $x+y=1$
(b) $x-y=1$
(c) $x+y+1=0$
(d) $x-y-2=0$

Answer 1

We have to use the standard equation of a line which is given by $\dfrac{x}{a}+\dfrac{y}{b}=1$ , where a and b are the X and Y intercepts respectively. We are given that the intercepts are equal, which gives $a=b$ . We have to substitute this value in the standard equation. Then, we have to find the value of a by substituting the coordinates of the given point in the resulting equation. Finally, we have to substitute the value of a in the resulting equation of the second step.

Complete step by step answer:
We have to find the equation of the line which passes through the point $\left( 1,-2 \right)$ and cuts off equal intercept from axes. We know that equation of a line is given by the formula
$\dfrac{x}{a}+\dfrac{y}{b}=1...\left( i \right)$
where a and b are the X and Y intercepts respectively.
We are given that the intercepts are equal.
$\Rightarrow a=b$
Therefore, we can write the equation (i) as
$\begin{aligned} & \Rightarrow \dfrac{x}{a}+\dfrac{y}{a}=1 \\\ & \Rightarrow \dfrac{x+y}{a}=1 \\\ & \Rightarrow x+y=a...\left( i \right) \\\ \end{aligned}$
We have to find the value of a. We are given that the line passes through the point $\left( 1,-2 \right)$ . Therefore, we have to substitute $x=1$ and $y=-2$ in the equation (ii).
$\begin{aligned} & \Rightarrow 1-2=a \\\ & \Rightarrow a=-1 \\\ \end{aligned}$
Now, we have to substitute the value of a in the equation (ii).
$\Rightarrow x+y=-1$
Let us take -1 to the LHS.
$\Rightarrow x+y+1=0$

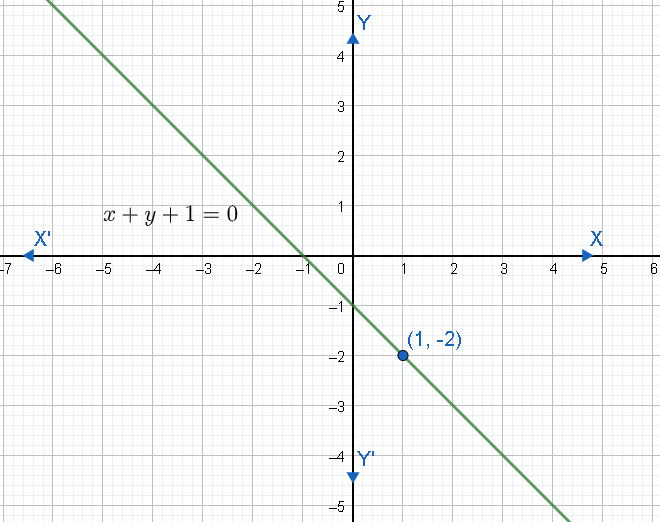
So, the correct answer is “Option c”.

Note: Students must be thorough with the equations of straight lines. There are many forms of equations of straight line such as slope-intercept form, point-slope form, two-point form, slope-intercept form, intercept form and normal form. We have used the intercept form in the above solution.