Question

The equation of a circle which passes through the origin and cuts off intercepts $4$ and $6$ on the axes is
(A) ${x^2} + {y^2} = 24$
(B) ${x^2} + {y^2} - 4x - 6y = 0$
(C) ${x^2} + {y^2} = 10$
(D) ${x^2} + {y^2} - 8x - 12y = 0$

Answer 1

Start with using the general equation of a circle. Now change the equation by satisfying the point $\left( {0,0} \right)$ and obtain a relation $c = 0$. Now from the newly formed equation, put $x = 0$ and $y = 0$ separately to find the expression for the intercepts in the above-obtained equation. Use this expression and the given value of intercepts to form a family of equations. Check which option satisfies the family.

Complete step by step answer:
Here we are given a problem where we need to find the equation of a circle which passes through the origin and makes an intercept of $4$ and $6$ on the axis. And with this information, we need to find the correct option from the given four options.
As we know that the equation ${x^2} + {y^2} + 2gx + 2fy + c = 0$ represents a circle whose centre is $\left( { - g, - f} \right)$ and having a radius of $\sqrt {{g^2} + {f^2} - c}$.
But it is given that the circle passes through the origin, i.e. $\left( {0,0} \right)$. The equation ${x^2} + {y^2} + 2gx + 2fy + c = 0$ should satisfy the point $\left( {0,0} \right)$
$\Rightarrow {\text{At }}\left( {0,0} \right){\text{; }}{{\text{0}}^2} + {0^2} + 2g \times 0 + 2f \times 0 + c = 0 \Rightarrow c = 0$
Therefore, we get that: $c = 0$, if the circle passes from the origin.
Thus, we get the required equation in the form: ${x^2} + {y^2} + 2gx + 2fy = 0$.
As we know that the intercepts are formed when the curve cuts the axis at some point. And when the curve touches the x-axis, the y-coordinate will become equal to zero and when the curve cuts the y-axis, the y-coordinate will become equal to zero.
When $y = 0$, we have:
$\Rightarrow {x^2} + 0 + 2gx + 0 = 0 \Rightarrow {x^2} + 2gx = 0$
This can also be further simplified by taking common :
$\Rightarrow {x^2} + 2gx = 0 \Rightarrow x\left( {x + 2g} \right) = 0$
This can also be written as:
$\Rightarrow x\left( {x + 2g} \right) = 0 \Rightarrow x = 0{\text{ or }}x = - 2g$
Now, since we already know that the point $\left( {0,0} \right)$ satisfies the equation, we can say:
${\text{At }}y = 0,{\text{ }}x = - 2g$
Similarly, when we put $x = 0$ in the equation ${x^2} + {y^2} + 2gx + 2fy = 0$, we will get: $y = - 2f$
Therefore, from this we get
$\Rightarrow {\text{ At }}x = 0,{\text{ }}y = - 2f{\text{ and at }}y = 0,{\text{ }}x = - 2g$
This defines the intercepts made by the curve as discussed in the above sections.
Since we already have the values of the intercepts as $4$ and $6$. Using this and the above conclusion, we can find a family of equations that satisfy these conditions.
As the intercepts $4$ and $6$ are length from the origin, which can be on both the negative or positive side of the axis.
When $4$ is taken as x-intercept and $6$ is taken as the y-intercept
$\Rightarrow {x^2} + {y^2} \pm 4x \pm 6y = 0$ represents a set of four equations of circle ......(i)
When $4$ is taken as y-intercept and $6$ is taken as the x-intercept
$\Rightarrow {x^2} + {y^2} \pm 6x \pm 4y = 0$ represents a set of four equations of circle ......(ii)

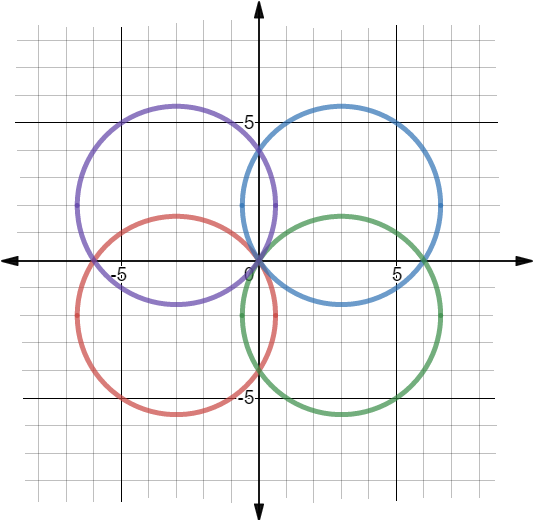
This figure represents the group of circles represented by the equation:
${x^2} + {y^2} \pm 4x \pm 6y = 0$

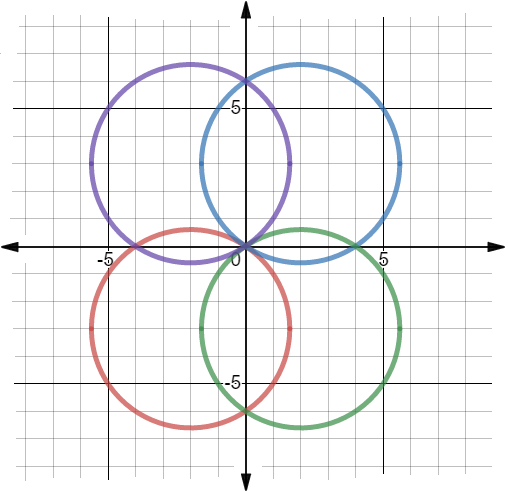
This second figure represents the group of circles represented by the equation:
${x^2} + {y^2} \pm 6x \pm 4y = 0$
Hence, the option (B), i.e. equation ${x^2} + {y^2} - 4x - 6y = 0$ is one of the equations represented by relation (i)

Thus, the option (B) is the correct answer.

Note:
An alternative approach can be taken by eliminating the options according to the given conditions. Like the condition that says $c = 0$ can eliminate options (A) and (C) from the correct choices. Then intercepts in both the remaining equations ${x^2} + {y^2} - 4x - 6y = 0$ and ${x^2} + {y^2} - 8x - 12y = 0$ can be easily found for obtaining the correct answer.