Question

The equation of a circle of radius $5$ which lies within the circle ${x^2} + {y^2} + 14x + 10y - 26 = 0$ and touches it at the point $\left( { - 1,3} \right)$ is
(A) ${x^2} + {y^2} + 8x + 2y + 8 = 0$
(B) ${x^2} + {y^2} + 8x + 2y - 8 = 0$
(C) ${x^2} + {y^2} + 8x + 2y - 14 = 0$
(D) None of these

Answer 1

In the above question, first we have to find the radius and center of the given circle by comparing it with the standard equation of circle. The standard equation of the circle is ${x^2} + {y^2} + 2gx + 2yf + c = 0$ and its center is $( - g, - f)$ and the radius is $r = \sqrt {{g^2} + {f^2} - c}$.

Complete answer:
In the above question, it is given that we have given a circle whose equation is ${x^2} + {y^2} + 14x + 10y - 26 = 0$ and there is another circle inside the given circle which touches it at $\left( { - 1,3} \right)$ and whose radius is $5$.

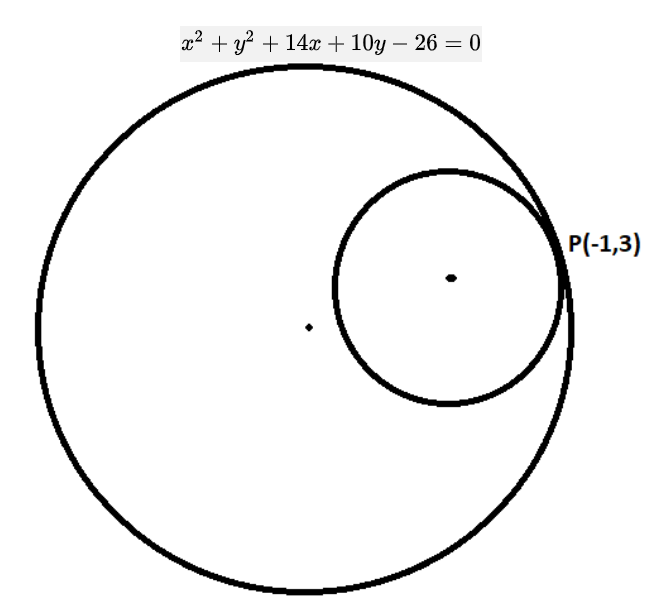
The equation of given circle is ${x^2} + {y^2} + 14x + 10y - 26 = 0$.
Now, we will compare it the standard equation of circle (${x^2} + {y^2} + 2gx + 2yf + c = 0$ , where $( - g, - f)$ is the center and the radius of the circle is $r = \sqrt {{g^2} + {f^2} - c}$).
Therefore, the center of the given circle is $\left( { - 7, - 5} \right)$ and the radius of the circle is $r = \sqrt {{{\left( { - 7} \right)}^2} + {{\left( { - 5} \right)}^2} - \left( { - 26} \right)}$
$r = \sqrt {49 + 25 + 26}$
$r = \sqrt {100}$
$r = 10$
If we note here, we will find that the radius of this circle is twice the radius of the required circle.
Therefore, the required circle is passing through the center of the given circle.
Hence, the center of the required circle is the midpoint of $\left( { - 1,3} \right)$ and $\left( { - 7, - 5} \right)$.
$h = \dfrac{{\left( { - 1} \right) + \left( { - 7} \right)}}{2},k = \dfrac{{3 + \left( { - 5} \right)}}{2}$
$h = \dfrac{{ - 8}}{2},k = \dfrac{{ - 2}}{2}$
$h = - 4,k = - 1$
Therefore, the center of the required circle is $h = - 4,k = - 1$ and its radius is $5$.
Hence the equation of required circle is ${\left( {x - \left( { - 4} \right)} \right)^2} + {\left( {y - \left( { - 1} \right)} \right)^2} = {\left( 5 \right)^2}$
$\Rightarrow {\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} = 25$
$\Rightarrow {x^2} + 16 + 8x + {y^2} + 1 + 2y = 25$
$\Rightarrow {x^2} + {y^2} + 8x + 2y - 8 = 0$
Therefore, it is the equation of the required circle.

Therefore, the correct option is (B).

Note: We can also find the equation of the required circle by using the diameter form of the equation of the circle. Here one point is given which is given on its circumference and the other point is the center of the given circle.