Question

The equation of a circle in parametric form is given by $x=a\cos \theta$ , $y=a\sin \theta$ . The locus of the point of intersection of the tangents to the circle, whose parametric angles differ by $\dfrac{\pi }{2}$ .
(A) ${{x}^{2}}+{{y}^{2}}=5{{a}^{2}}$
(B) ${{x}^{2}}+{{y}^{2}}=2{{a}^{2}}$
(C) ${{x}^{2}}+{{y}^{2}}=3{{a}^{2}}$
(D) ${{x}^{2}}+{{y}^{2}}=4{{a}^{2}}$

Answer 1

Hint: Assume that A and B are the points of the tangency and the parametric angle of point A be $\theta$ and point B be $\beta$ and the point of intersection of the tangents is P. The difference between the parametric angles $\beta$ and $\theta$ is equal to $\dfrac{\pi }{2}$ . Now, get the value of $\beta$ in terms of $\theta$ . The parametric form of a point on the circle can be represented by $x=a\cos \theta$ and $y=a\sin \theta$ . Now, get the parametric coordinates of point A and point B. Square and add the x-coordinate and y coordinate of the parametric coordinate of the point on the circle. The equation of the circle is ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ . We know the formula, the equation of the tangent at the point $\left( {{x}_{1}},{{y}_{1}} \right)$ of the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ is given by, $x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}$ . Now, using this formula, get the parametric coordinates of the points A and B and get the equation of the tangents at the point A and B of the circle. Now, square the equations of the tangents AP and BP and add them. Solve it further and get the equation of the point of intersection of the tangents AP and BP.

Complete step-by-step answer:
First of all, let us assume that A and B are the points of the tangency and the parametric angle of point A be $\theta$ and point B be $\beta$ and the point of intersection of the tangents is P.
According to the question, it is given that the difference between the parametric angles of point A and point B is $\dfrac{\pi }{2}$ . So,
$\beta -\theta =\dfrac{\pi }{2}$
$\Rightarrow \beta =\dfrac{\pi }{2}+\theta$ ………………………….(1)
It is also given that the parametric form of a point on the circle can be represented by
$x=a\cos \theta$ ……………………………(2)
$y=a\sin \theta$ ……………………………(3)
Since the parametric coordinate $\left( a\cos \theta ,asin\theta \right)$ lies on the circle, so it must satisfy the equation of the circle.
On squaring equation (2) and equation (3), we get
${{x}^{2}}={{a}^{2}}\cos \theta$ ………………………….(4)
${{y}^{2}}={{a}^{2}}\sin \theta$ ………………………….(5)
On adding equation (4) and equation (5), we get
${{x}^{2}}+{{y}^{2}}={{a}^{2}}{{\cos }^{2}}\theta +{{a}^{2}}{{\sin }^{2}}\theta$
${{x}^{2}}+{{y}^{2}}={{a}^{2}}\left( {{\cos }^{2}}\theta +{{\sin }^{2}}\theta \right)$ …………………………..(6)
We know the identity, ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$ …………………………….(7)
From equation (6) and equation (7), we get
${{x}^{2}}+{{y}^{2}}={{a}^{2}}.1$
$\Rightarrow {{x}^{2}}+{{y}^{2}}={{a}^{2}}$
Now, we have got our equation of the circle, ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ .
We know the equation of the tangent at the point $\left( {{x}_{1}},{{y}_{1}} \right)$ of the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ is given by,
$x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}$ ………………….(8)
The parametric angle of point and point B is $\theta$ and $\beta$ .
The coordinate of point A = $\left( a\cos \theta ,asin\theta \right)$ …………………………..(9)
From equation (1), we have the value of $\beta$ .
Now, the coordinate of point B = $\left( a\cos \left( \dfrac{\pi }{2}+\theta \right),asin\left( \dfrac{\pi }{2}+\theta \right) \right)$ ………………………………(10)

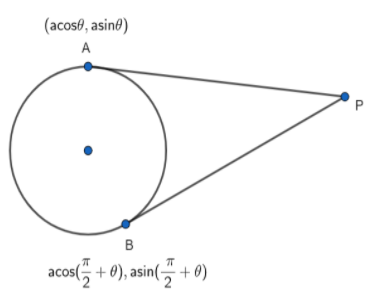
Using equation (8), we can get the equation of the tangent of the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ at point A.
Now, the equation of the tangent at point A i.e, AP
$x\left( a\cos \theta \right)+y\left( a\sin \theta \right)={{a}^{2}}$
$\Rightarrow x\cos \theta +y\sin \theta =a$ ……………………………(11)
Similarly, using equation (8), we can get the equation of the tangent of the circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ at point B.
Now, the equation of the tangent at point B i.e, BP
x\left\\{ a\cos \left( \dfrac{\pi }{2}+\theta \right) \right\\}+y\left\\{ asin\left( \dfrac{\pi }{2}+\theta \right) \right\\}={{a}^{2}}
$\Rightarrow x.\cos \left( \dfrac{\pi }{2}+\theta \right)+y.sin\left( \dfrac{\pi }{2}+\theta \right)=a$ ……………………………(12)
We know that, $\cos \left( \dfrac{\pi }{2}+\theta \right)=-\sin \theta$ and $sin\left( \dfrac{\pi }{2}+\theta \right)=\cos \theta$ …………………….(13)
From equation (12) and equation (13), we get
$\Rightarrow x\left( -\sin \theta \right)+y\left( \cos \theta \right)=a$
$\Rightarrow -x\sin \theta +y\cos \theta =a$ ………………………..(14)
Since the tangents at points A and B are meeting at point P so, the point P must satisfy the equation of the tangent AP and BP.
Now, squaring equation (11) and equation (14), and adding then we get

& \Rightarrow {{\left( x\cos \theta +y\sin \theta \right)}^{2}}+{{\left( -x\sin \theta +y\cos \theta \right)}^{2}}={{a}^{2}}+{{a}^{2}} \\\ & \Rightarrow {{x}^{2}}{{\cos }^{2}}\theta +{{y}^{2}}{{\sin }^{2}}\theta +2x\cos \theta .y\sin \theta +{{x}^{2}}{{\sin }^{2}}\theta +{{y}^{2}}{{\cos }^{2}}\theta +2\left( -x\sin \theta \right).y\cos \theta =2{{a}^{2}} \\\ & \Rightarrow {{x}^{2}}{{\cos }^{2}}\theta +{{x}^{2}}{{\sin }^{2}}\theta +{{y}^{2}}{{\sin }^{2}}\theta +{{y}^{2}}{{\cos }^{2}}\theta +2xy\cos \theta \sin \theta -2xy\cos \theta \sin \theta =2{{a}^{2}} \\\ \end{aligned}$$ $$\Rightarrow {{x}^{2}}\left( {{\cos }^{2}}\theta +{{\sin }^{2}}\theta \right)+{{y}^{2}}\left( {{\cos }^{2}}\theta +{{\sin }^{2}}\theta \right)=2{{a}^{2}}$$ …………………………..(15) From equation (7) and equation (15), we get $$\begin{aligned} & \Rightarrow {{x}^{2}}.1+{{y}^{2}}.1=2{{a}^{2}} \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}=2{{a}^{2}} \\\ \end{aligned}$$ Therefore, the locus of the point of intersection is $${{x}^{2}}+{{y}^{2}}=2{{a}^{2}}$$ . Hence, option (B) is the correct one. Note: In this question, one might take the parametric angle of point A as $$\theta $$ and point B as $$\left( \dfrac{\pi }{2}-\theta \right)$$ . This is wrong because it is given that the difference between the parametric angles of points A and B should be $$\dfrac{\pi }{2}$$ . But here, the difference is, $$\begin{aligned} & \theta -\left( \dfrac{\pi }{2}-\theta \right) \\\ & =\theta +\theta -\dfrac{\pi }{2} \\\ & =2\theta -\dfrac{\pi }{2} \\\ \end{aligned}$$ We can see that the difference between the parametric angles of points A and B is not equal to $$\dfrac{\pi }{2}$$ .