Question

The equation 2tan x + 5x - 2 = 0 has:
$\left( a \right){\text{No solution in }}\left[ {0,\dfrac{\pi }{4}} \right] \\\ \left( b \right){\text{At least one real solution in }}\left[ {0,\dfrac{\pi }{4}} \right] \\\ \left( c \right){\text{Two real solution in }}\left[ {0,\dfrac{\pi }{4}} \right] \\\ \left( d \right)\,{\text{None of these}} \\\$

Answer 1

Hint- In this question, we use the graphical method to find a solution. To find a solution we have to plot a graph of two curves and then observe their point of intersection. Graphical method points of intersections of curves tell the number of solutions and also give the coordinate of intersection points.

Complete step-by-step solution -
Given, we have an equation $2\tan x + 5x - 2 = 0$
We know it’s impossible to solve trigonometric terms (tanx) with linear terms (x) so we can separate them like one side of the equation has a trigonometric term and the other side of the equation has a linear term.
$\Rightarrow \tan x = \dfrac{{ - 5x + 2}}{2} \\\ \Rightarrow \tan x = - \dfrac{{5x}}{2} + 1 \\\$
We assume $y = \tan x{\text{ and }}y = - \dfrac{{5x}}{2} + 1$
The functions $y = \tan x{\text{ and }}y = - \dfrac{{5x}}{2} + 1$ can be plotted on the same graph and solution of equation $2\tan x + 5x - 2 = 0$ is intersection of two curves.
Now, first we plot a graph of tanx and we want a solution in the domain of $\left[ {0,\dfrac{\pi }{4}} \right]$ .

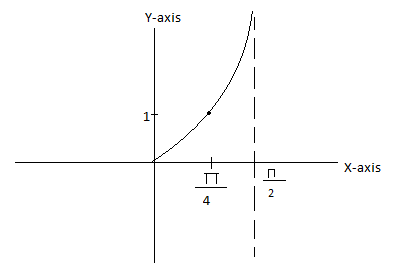
Now, we plot the graph of ${\text{ }}y = - \dfrac{{5x}}{2} + 1$

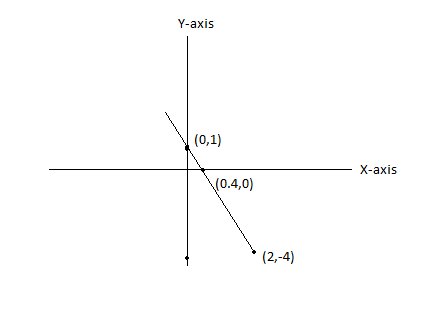
From the graph, it is seen that the line intersects the x-axis at $x = \dfrac{2}{5}$
Now, we see the intersection points of the two curves.

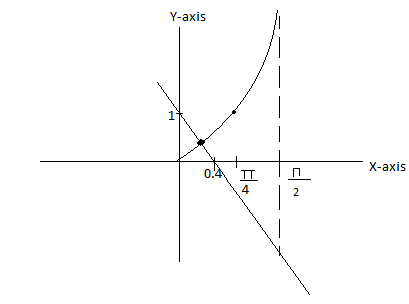
For some x such that $0 < x < \dfrac{2}{5}$ , two curves meet at one point.
Since, $0 < \dfrac{2}{5} < \dfrac{\pi }{4}$
For the value of $x \in \left[ {0,\dfrac{\pi }{4}} \right]$ ,both curves intersect at only one point.
So, the correct option is (b).

Note- In such types of problems we use some important points to solve questions in an easy way. First we separate the trigonometric and linear term by taking linear terms on one side of the equation and then draw their graphs. Then observe their point of intersection on graphs. So, the solution of such types of problems is the point of intersection of curves.