Question

The engine of a motorcycle can produce a maximum acceleration of $5$m/s2. Its brakes can produce a maximum retardation $10m/{s^2}$. If motorcyclists start from point A and reach point B. What is the minimum time in which it can cover if the distance between A and B is $1.5$km? (Given: that motorcycle comes to rest at B)
A.30 seconds
B.15 seconds
C.10 seconds
D.5 seconds

Answer 1

In the above problem we have to calculate the time to travel to whorl journey, but we see that the motorcycle is not having a constant acceleration. So, I will split the time also. We will calculate the time taken when the acceleration was $5m/{s^2}$ and when the retardation by the brake was $10m/{s^2}$ separately .

Complete answer:
S we will prepare a graph which is showing the motorcycle is travelling the distance with acceleration of $5m/{s^2}$ in time $t$ and after that motorcycle is travelling the remaining distance with a retardation of $10m/{s^2}$ in time $T - t$. So, the total time needed to cover the whole distance will be $T$. The maximum velocity is also shown in the graph below.

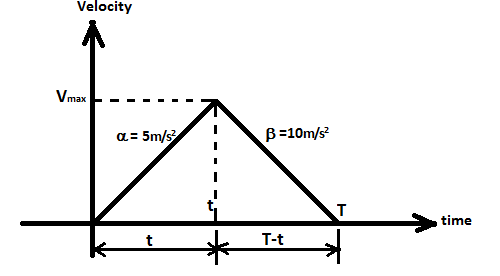
To solve the above problem, we will go through the sequence of steps as follows,
Firstly, we will write the expression for the area of the velocity triangle which will be equal to the total distance.
So, $S = \dfrac{1}{2} \times T \times {V_{\max }}$ --------equation (1)
Now we will find the maximum velocity as follows,
${V_{\max }} = u + \alpha t$, (since the motorcycle covers its maximum speed in time $t$ with acceleration $\alpha$)
Also, the initial velocity is zero.
So, now, $\Rightarrow {V_{\max }} = \alpha t$-----equation (2)
Now for the time interval $T - t$,
$v = u + at$
Since the final velocity is given to be zero as the motorcycle comes to rest at final point B. during his time interval $(T - t)$the retardation is $\beta$, So the equation will be as follows,
$\Rightarrow 0 = {V_{\max }} - \beta (T - t)$
$\Rightarrow {V_{\max }} = \beta (T - t)$-----equation (3)
Now equating both the equations, equation (2) and equation (3)
$\Rightarrow \alpha t = \beta (T - t)$
$\Rightarrow \alpha t = \beta T - \beta t$
$\Rightarrow \alpha t + \beta t = \beta T$
$\Rightarrow t(\alpha + \beta ) = \beta T$
$\Rightarrow t = \dfrac{{\beta T}}{{(\alpha + \beta )}}$------equation (4)
Now putting ${V_{\max }}$from equation (2) in the equation (1), we get,
$\Rightarrow S = \dfrac{1}{2} \times T \times (\alpha t)$
Now putting the value of the time $t$ from equation (4), we get
$\Rightarrow S = \dfrac{1}{2} \times T \times \left[ {\alpha \left( {\dfrac{{\beta T}}{{(\alpha + \beta )}}} \right)} \right]$
$\Rightarrow S = \dfrac{1}{2} \times {T^2} \times \left[ {\dfrac{{\alpha \beta }}{{(\alpha + \beta )}}} \right]$
Now putting the values, $S = 1.5Km = 1500m$, $\alpha = 5m/{s^2}$, $\beta = 10m/{s^2}$, we get
$\Rightarrow 1500 = \dfrac{1}{2} \times {T^2} \times \left[ {\dfrac{{5 \times 10}}{{(5 + 10)}}} \right]$
$\Rightarrow 3000 = {T^2} \times \left[ {\dfrac{{50}}{{15}}} \right]$
$\Rightarrow \dfrac{{3000 \times 15}}{{50}} = {T^2}$
$\Rightarrow \dfrac{{300 \times 15}}{5} = {T^2}$
$\Rightarrow 300 \times 3 = {T^2}$
$\Rightarrow 900 = {T^2}$
$\Rightarrow {T^2} = 900$
$\Rightarrow T = \sqrt {900}$
$\Rightarrow T = 30$second
Hence, in the above given problem the minimum time in which a motorcycle can cover if the distance between A and B is $1.5$km is 30 seconds.

So, option (A) is the correct answer.

Note:
During solving we have taken the above graph which is having a triangular shape not some other shape like trapezium. The reason behind this is that the triangular shape of the same area as that of the trapezium will have the base less than the trapezium, and the base of the triangle will represent the total time. Hence taking triangle shape will give the small base results in the minimum time to cover the same distance and here in the question it is asked for the minimum time.