Question

The ends of the rods of length ‘l’ move on the coordinate axes. The locus of the point on the rod which divides it in ratio 1:2 is
a. $9{{x}^{2}}+36{{y}^{2}}=144$
b. $9{{x}^{2}}+36{{y}^{2}}=l$
c. $36{{x}^{2}}+9{{y}^{2}}=l$
d. $9{{x}^{2}}+36{{y}^{2}}=4{{l}^{2}}$

Answer 1

Hint: We consider the variable rod whose ends are on the coordinate axes are A, B .Consider the rod as a line and represent its equation in intercept form. Consider a variable point C on the rod as (h,k) which divides the point A and B in the ratio 1:2. Find the expression of h and k in terms of a and b, where a and b are the intercept cut by the rod on the coordinate axes. Eliminate a and b using the information that the length of the rod is l. Replace (h,k) by (x,y) to get the required locus.

Complete step-by-step answer:
Given that, the ends of the rods lie on the coordinate axis. Therefore, let’s consider the ends of the rod as A(0,b), B(a,0) , where the a and b are parameters. Therefore, the length of the rod is given by $l=\sqrt{{{a}^{2}}+{{b}^{2}}}$ . So, the equation of the rod (line) in intercept form can be given as $\dfrac{x}{a}+\dfrac{y}{b}=1$ .
To proceed with the solution, first, we will represent the given line on a graph.

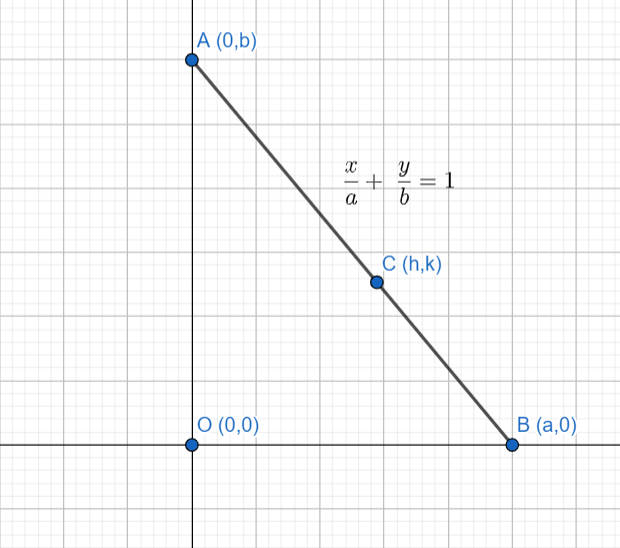
Given that, the length of the rod is $l$ . So, AB = l . Now, from the figure, we can see that OAB is a right-angled triangle, with OB = a , OA = b and AB = l . As OAB is a right-angled triangle, by Pythagoras theorem, we can say $O{{A}^{2}}+O{{B}^{2}}=A{{B}^{2}}$ .
$\Rightarrow {{b}^{2}}+{{a}^{2}}={{l}^{2}}$
$\Rightarrow l=\sqrt{{{a}^{2}}+{{b}^{2}}}$ $....(1)$
It is given that a variable point C(h,k) divides the line segment AB in ratio the ratio 1:2.
Now, we know that the point R $\left( x,y \right)$ , which divides the line joining the two points P $\left( {{x}_{1}},{{y}_{1}} \right)$ and Q $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $\left( x,y \right)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ . Now, C(h,k) divides the line segment AB in ratio the ratio 1:2. On using the formula, we get $C=\left( \dfrac{\left( 1\times a \right)+\left( 2\times 0 \right)}{1+2},\dfrac{\left( 1\times 0 \right)+\left( 2\times b \right)}{1+2} \right)$ .
$\Rightarrow C=\left( \dfrac{a}{3},\dfrac{2b}{3} \right)$
But we considered the coordinates of C as (h,k). On comparing with $C=\left( \dfrac{a}{3},\dfrac{2b}{3} \right)$ , we get $h=\dfrac{a}{3}$ and $k=\dfrac{2b}{3}$ .
$\Rightarrow a=3h,\text{ }2b=3k.....(2)$
Now, we know, the length of the rod is given as $l=\sqrt{{{a}^{2}}+{{b}^{2}}}$ . Substituting a = 3h and $b=\dfrac{3k}{2}$ , we get:$l=\sqrt{{{(3h)}^{2}}+{{\left( \dfrac{3k}{2} \right)}^{2}}}$
$\Rightarrow l=\sqrt{9{{h}^{2}}+\dfrac{9{{k}^{2}}}{4}}$
On squaring both sides, we get ${{l}^{2}}=9{{h}^{2}}+\dfrac{9{{k}^{2}}}{4}$
$\Rightarrow 4{{l}^{2}}=36{{x}^{2}}+9{{y}^{2}}.........\left( 3 \right)$
Now, the locus of C(h,k) is given by replacing (h,k) by (x,y) in equation (3). So, we get $4{{l}^{2}}=36{{x}^{2}}+9{{y}^{2}}$ .
Therefore, the locus of the variable point which divides the rod in the ratio 1:2 is $4{{l}^{2}}=36{{x}^{2}}+9{{y}^{2}}$ .
Therefore, option (d) is correct.

Note: This problem can also be done by using the following formula:
The ends of the rods of length ‘l’ moves on the coordinate axes and there exist a variable point P(x,y) which divides the ends in m:n ratio then the locus of the point is given by:
${{\left( \dfrac{mnl}{m+n} \right)}^{2}}={{n}^{2}}{{x}^{2}}+{{m}^{2}}{{y}^{2}}$