Question

The ends of major axis of an ellipse are $(5,0);(-5,0)$ and one of the foci lies on $3x-5y-9=0$, then the eccentricity of the ellipse is: -
$\begin{aligned} & a)\,\dfrac{2}{3} \\\ & b)\,\dfrac{3}{5} \\\ & c)\,\dfrac{4}{5} \\\ & d)\,\dfrac{1}{3} \\\ \end{aligned}$

Answer 1

Draw a rough diagram of an ellipse whose major axis lies on x-axis. Assume the general equation of the ellipse as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and find the value of ‘a’ using the given information about ends of major axis. Now, substitute the coordinates of foci i.e. (ae, o) in the equation $3x-5y-9=0$, to find the value of eccentricity; ‘e’

Complete step by step answer:
Here, we have been provided with an ellipse whose ends of major axes are $(5,0);(-5,0)$. It is said that one of the foci lies on the line $3x-5y-9=0$ and we have to determine the eccentricity of the ellipse. Now we know that general equation of an ellipse is given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ where ‘a’ is length so semi-major axis and ‘y’ is the length of semi-minor axis also called conjugate axis. Now. Drawing a graph of the general equation of an ellipse, we have,

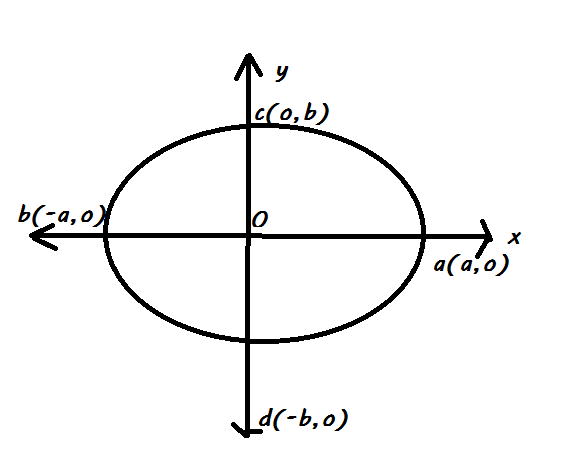
In the above figure, we can see that the endpoints of the major axis of an ellipse is given as $a(a,o)\,\text{and}\,b(-a,o)$. So, an comparing with the coordinates of ends of major axis given in the question, we have,
$\Rightarrow a=5...................(i)$
Now from the above figure we can see that there are two focus of an ellipse ${{s}_{1}}(ae,o)\,\text{and }\,{{\text{s}}_{2}}(-ae,o)$where ‘e’ is called the eccentricity of the ellipse. In the above question we have been said that one of the foci lies on $3x-5y-9=0$ so we have to find if it is ${{s}_{1\,\,}}\text{or }\,{{\text{s}}_{2}}$Therefore, drawing the graph of given line, we have,

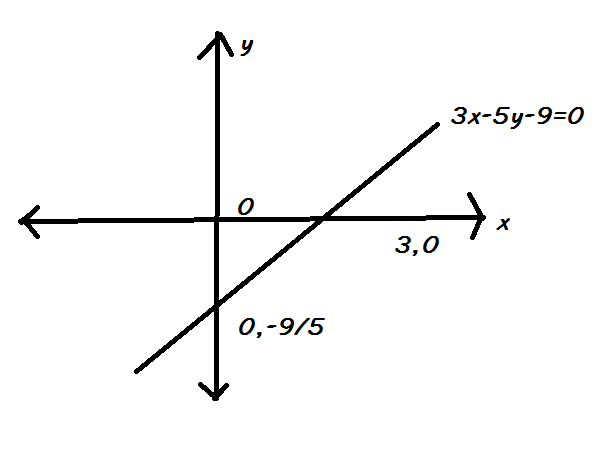
From the above graph clearly, we can see that the line is cutting the positive x-axis, therefore we conclude that ${{s}_{1}}$ is the focus that lies on this given line. Now, if ${{s}_{1}}$ lies on this line then its coordinate must satisfy the equation of line. So, substituting its coordinate must satisfy the equation of line. So, substituting${{s}_{1}}(ae,o)$ in the equation $3x-5y-9=0$ we get,
$\begin{aligned} & \Rightarrow 3(ae)-5\times 0-9=0 \\\ & \Rightarrow 3\times 5\times e-9=0\,(\text{using equation (i))} \\\ & \Rightarrow \text{15e=9} \\\ & \Rightarrow e=\dfrac{9}{15} \\\ & \Rightarrow e=\dfrac{3}{5} \\\ \end{aligned}$

So, the correct answer is “Option b”.

Note: One may note that there are two types of ellipse, one in which major axis lies on x-axis and the other in which major axis lies on y-axis. Here, we have been given that the end-points of the major axis was $(5,0);(-5,0)$ in which we can clearly see that y-coordinate is $0$ and this is the reason why we chose the x-axis as the major axis. Now, it is very important to determine whether ${{s}_{1}}\,\text{or}\,{{s}_{2}}$ lies on the given line, so you must draw the graph for this purpose. In the above solution if we would have substituted ${{s}_{2}}$ In the given line then we would have obtained a negative value of ‘e’ which is not possible.