Question

The end of a uniform wire of length L and of weight W is attached to a point on the roof and a weight ${{W}_{1}}$ is suspended from its lower end. If ‘S’ is the area of the cross section of the wire, what will be the stress on the wire at a height ($\dfrac{3L}{4}$) from its lower end?

& A.\text{ }\dfrac{{{W}_{1}}}{S} \\\ & B.\text{ }\dfrac{{{W}_{1}}+\dfrac{W}{4}}{S} \\\ & C.\text{ }\dfrac{{{W}_{1}}+\dfrac{3W}{4}}{S} \\\ & D.\text{ }\dfrac{{{W}_{1}}+W}{S} \\\ \end{aligned}$$

Answer 1

The stress experienced on the wire is due to the weight of the wire and the weight suspended from it. The stress is the force experienced per unit area of the material. The force is directed vertically, so no horizontal components have to be considered.
Formula Used:
The stress can be calculated as –
$Stress,\text{ }\gamma \text{=}\dfrac{Force}{Unit\text{ }Area}$

Complete answer:
The force experienced by a wire at any point is the product of its length from the desired end point and the weight of the total wire. This gives the tension experienced by the wire at a point.
Now, we are given that the wire has an additional weight hanging on it other than its own weight. This will surely add to the tension directly.

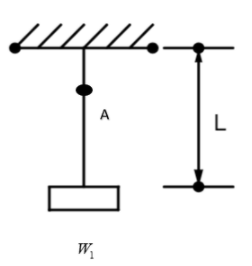
The tension experienced by the same wire at the bottom end is just due to the weight of the hanging box.
From the sketch of the discussing wire, we can see that ${{W}_{1}}$ hangs on the wire of weight W from a length of L from the roof with a surface area S.
Now, let us consider the tension on the rope. We can see clearly that the weight hanging on the wire contributes to the tension on the wire.
So, let us calculate the tension on the wire as – The total Tension is equal to the weight hanging added to the weight of the part of the wire involved, i.e., from point A. The weight of wire contributing to the tension from point A is $\dfrac{(\dfrac{3L}{4}\times \text{W)}}{L}\text{--(1)}$
Now the tension is from (1) – $Tension,\text{ T = }{{\text{W}}_{1}}\text{+}\dfrac{3}{4}\text{W -------(2)}$
Now, we can calculate the stress involved at point A of the wire.
$Stress,\text{ }\gamma \text{=}\dfrac{Tension}{Unit\text{ }Area}$
$\gamma \text{=}\dfrac{T}{S}\text{ -------(3)}$
From (1), (2) and (3),
$\Rightarrow \gamma \text{=}\dfrac{{{\text{W}}_{1}}\text{+}\dfrac{3}{4}\text{W}}{S}$
i.e., The stress experienced by the rope at point A $\dfrac{3L}{4}$ from the bottom is $\Rightarrow \gamma \text{=}\dfrac{{{\text{W}}_{1}}\text{+}\dfrac{3}{4}\text{W}}{S}$

The answer is option C.

Note:
The weight of the hanging material contributes to most of the tension on the wire. For thin wires of very small cross-sectional area, with less weight, we usually neglect the weight of the wire. In some questions the missing details about the wire can be taken this way.