Question

The empty space in this hcp unit cell is:
A) $74\%$
B) $47.6\%$
C) $32\%$
D) $26\%$
​

Answer 1

To answer this question you should recall the concept of close packing in a solid crystal. Voids refer to the gaps between the constituent particles. These voids in solid crystals mean the vacant space between the constituent particles. It can be calculated from the formula (given below).

Formula used:
${\text{Packing fraction}} = \dfrac{{{\text{Total volume of unit cell}}}}{{{\text{Volume occupied}}}}$

Complete step by step solution:
The unit cells are systematically arranged in such a way that fills the space without overlapping. A crystal lattice can be defined as the 3D arrangement of atoms, molecules or ions inside a crystal. Each unit of this crystal lattice is known as a unit cell. These crystal lattices can be broadly classified into primitive cubic, body-centred cubic (BCC) or face-centred cubic (FCC). In the question, we are asked to find space in the hcp unit cell. The crystal lattice of hcp unit cell can be drawn as:

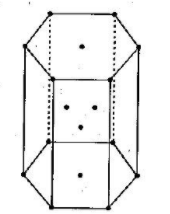
We know that the formula for packing fraction can be written as
${\text{Packing fraction}} = \dfrac{{{\text{Total volume of unit cell}}}}{{{\text{Volume occupied}}}}$
Substituting the values of occupied sphere and volume of the unit cell we have:
$\Rightarrow \dfrac{{6 \times \dfrac{4}{3} \times \pi {r^3}}}{{24\sqrt 2 {r^3}}} = 0.74$
Rearranging and solving:
$\% {\text{ occupied space}} = 74\%$
The space in the hcp unit cell = $100 - 74 = 26\%$.

Hence, the correct option is option D.

Note:
Crystalline solids show regular and repeating pattern arrangement of constituent particles resulting in two types of interstitial voids in a 3D structure:

1. Tetrahedral voids: In case of a cubic close-packed structure, the second layer of spheres is present over the triangular voids of the first layer. This results in each sphere touching the three spheres of the first layer. When we join the centre of these four spheres, we get a tetrahedron and the space left over by joining the centre of these spheres forms a tetrahedral void.
2. Octahedral voids: Adjacent to tetrahedral voids you can find octahedral voids. When the triangular voids of the first layer coincide with the triangular voids of the layer above or below it, we get a void that is formed by enclosing six spheres. This vacant space which is formed by the combination of the initial formed triangular voids of the first layer and that of the second layer is known as Octahedral Voids.