Question

The emf of the battery shown in the figure is

(A) $12V$
(B) $16V$
(C) $18V$
(D) $15V$

Answer 1

Hint : In the electrical circuit given in the above question we need to find $E$ in volts. We will use resistance simplification and Kirchhoff’s Voltage and Current Laws. We will use $V = IR$ , where $V$ is the voltage drop across a resistor along the direction of current flow, $R$ is the resistance to be used from the diagram given, and $I$ is the current through the specific resistance.

Formula Used: ${\text{Voltage = Current}} \times {\text{Resistance}}$

Complete step by step answer
Let us assume the notation ${V_{xy}}$ to denote the voltage drop between two points, say ${V_x}$ and ${V_y}$ .
We redraw the diagram adding the two resistances in series in the right-most branch. The formula for a series combination of resistances is
$\Rightarrow {R_{net}} = {R_1} + {R_2} + ...$
Here ${R_{net}} = 2\Omega + 1\Omega = 3\Omega$ as shown in the figure.

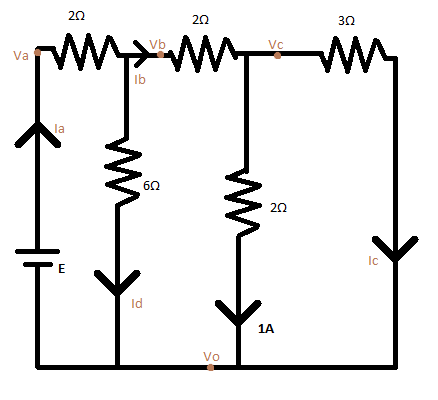
Using $V = IR$ across the $2\Omega$ resistor through which $1A$ current is flowing, we get
$\Rightarrow {V_{co}} = 1A \times 2\Omega = 2V$
$\therefore {I_c} = \dfrac{{{V_{co}}}}{{3\Omega }} = \dfrac{{2V}}{{3\Omega }} = \dfrac{2}{3}A$
Applying Kirchhoff’s Circuit Law again we get
$\Rightarrow {I_b} = 1A + {I_c} = 1A + \dfrac{2}{3}A = \dfrac{5}{3}A$
Now to get ${V_{bc}}$ , we use $V = IR$ across the resistor through which current ${I_b}$ is flowing.
$\Rightarrow {V_{bc}} = {I_b} \times 2\Omega = \dfrac{5}{3}A \times 2\Omega = \dfrac{{10}}{3}V$ .
$\therefore {V_{bo}} = {V_{bc}} + {V_{co}} = \dfrac{{10}}{3}V + 2V = \dfrac{{16}}{3}V$
Now we can calculate ${I_d}$ as,
$\Rightarrow {I_d} = \dfrac{{{V_{bo}}}}{{6\Omega }} = \dfrac{{\dfrac{{16}}{3}V}}{{6\Omega }} = \dfrac{8}{9}A$
Applying Kirchhoff’s Circuit Law again we get
$\Rightarrow {I_a} = {I_b} + {I_d}$
$\Rightarrow {I_a} = \dfrac{5}{3}A + \dfrac{8}{9}A = \dfrac{{23}}{9}A$
Applying $V = IR$ across the resistor through which current ${I_a}$ is flowing, we get
$\Rightarrow {V_{ab}} = {I_a} \times 2\Omega = \dfrac{{23}}{9}A \times 2\Omega = \dfrac{{46}}{9}V$
Therefore we can say that,
$\Rightarrow {V_{ao}} = {V_{ab}} + {V_{bo}}$
$\Rightarrow {V_{ao}} = \dfrac{{46}}{9}V + \dfrac{{16}}{3}V = \dfrac{{94}}{9}V$
From the diagram, we see that the voltage drop across the battery is the same as the voltage drop between ${V_a}$ and ${V_o}$ . Thus, since $E = {V_{ao}}$ , the emf of the battery is $E = \dfrac{{94}}{9}V = 10.444V \approx 12V$ . We approximate the voltage since it is the closest option as given in the question. Also, the voltage drop across the battery will be less than the emf of the battery due to the internal resistance of a battery. Thus the emf is equal to the voltage drop only in the ideal case.
The correct option is (A) $12V$ .

Note
We can also calculate $E = {V_{ao}}$ by applying Kirchhoff’s Voltage Law along the path $a - b - c - o - a$ . This way we will get the same result. The other ways of calculating $E$ from the same figure using different paths are $a - b - o - a$ and $a - b - c - o - a$ . In each of these processes, we will require the current in each of the resistors involved in the circuit and so we have chosen the above process.