Question

The ellipse ${{x}^{2}}+4{{y}^{2}}=4$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point $\left( 4,0 \right)$. Then the equation of the ellipse is
(A)${{x}^{2}}+12{{y}^{2}}=16$
(B)$4{{x}^{2}}+48{{y}^{2}}=48$
(C)$4{{x}^{2}}+64{{y}^{2}}=48$
(D)${{x}^{2}}+16{{y}^{2}}=16$

Answer 1

To solve this problem we need to concept of ellipse and analyse the figure with the various values which are given in the question. The generalised equation of the ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, where $a$ and $b$ are the major and minor axis respectively when centre is $\left( 0,0 \right)$. The figure explains the problem in a much efficient manner.

Complete step-by-step solution:
The question ask us to find the equation of the ellipse into which a rectangle is inscribed inside which another ellipse of equation ${{x}^{2}}+4{{y}^{2}}=4$ is inscribed where rectangle is aligned with the co-ordinate axis.
The equation of the ellipse given is ${{x}^{2}}+4{{y}^{2}}=4$, which can be written as $\dfrac{{{x}^{2}}}{4}+\dfrac{4{{y}^{2}}}{4}=\dfrac{4}{4}$ which on calculation becomes
$\Rightarrow \dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{1}=1$
$\Rightarrow \dfrac{{{x}^{2}}}{{{2}^{2}}}+\dfrac{{{y}^{2}}}{{{1}^{2}}}=1$
On seeing the equation we can infer that the 2 coordinates are$\left( 2,0 \right)$ and $\left( 0,1 \right)$ of longer and shorter axes respectively. To analyse it in more proper way we can have can see the diagram

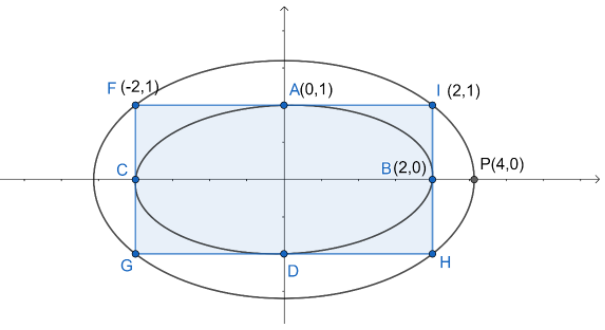
We know the coordinates of the which would help in finding the equation for the ellipse. The point known to us is $P\left( 4,0 \right)$. We know that the general form of equation for ellipse is
$\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, here $a$ is the major axis while $b$ is the minor axis.
Since the coordinate for $P$ is given so $a=4$ .The centre of all the three conic section is $\left( 0,0 \right)$ so the equation of the ellipse become
$\Rightarrow \dfrac{{{x}^{2}}}{{{4}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
The next step is to find the value of $b$ which is the minor axis. Since we know that the point $I$ , a vertex of the rectangle lies on the larger ellipse so it will satisfy the above equation. On putting the coordinates of $I$ in the equation of ellipse we get:
$\Rightarrow \dfrac{{{2}^{2}}}{{{4}^{2}}}+\dfrac{{{1}^{2}}}{{{b}^{2}}}=1$
$\Rightarrow \dfrac{4}{16}+\dfrac{1}{{{b}^{2}}}=1$
$\Rightarrow \dfrac{1}{{{b}^{2}}}=1-\dfrac{4}{16}$
On calculating the above equation we get:
$\Rightarrow \dfrac{1}{{{b}^{2}}}=\dfrac{16-4}{16}$
$\Rightarrow \dfrac{1}{{{b}^{2}}}=\dfrac{12}{16}$
$\Rightarrow {{b}^{2}}=\dfrac{16}{12}$
$\Rightarrow b=\dfrac{4}{\sqrt{12}}$
Now putting the value in the equation get:
$\Rightarrow \dfrac{{{x}^{2}}}{{{4}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
$\Rightarrow \dfrac{{{x}^{2}}}{{{4}^{2}}}+\dfrac{{{y}^{2}}}{{{\left( \dfrac{4}{\sqrt{12}} \right)}^{2}}}=1$
$\Rightarrow \dfrac{{{x}^{2}}}{{{4}^{2}}}+\dfrac{12{{y}^{2}}}{{{4}^{2}}}=1$
$\Rightarrow {{x}^{2}}+12{{y}^{2}}=16$
$\therefore$ The equation of the bigger ellipse is (A)${{x}^{2}}+12{{y}^{2}}=16$.

Note: We can check whether the equation of ellipse is correct or not. For this we will put the coordinates of the other vertex of the rectangle in the equation of the ellipse and if the L.H.S becomes equal to R.H.S. The equation of the ellipse is correct. Let's put the coordinate of $F\left( -2,1 \right)$ in the equation ${{x}^{2}}+12{{y}^{2}}=16$ we got. On putting the value we get
$\Rightarrow {{\left( -2 \right)}^{2}}+12{{\left( 1 \right)}^{2}}=16$
$\Rightarrow 4+12=16$
$\Rightarrow 16=16$
Since L.H.S is equal to R.H.S so the equation of the ellipse we found is correct.