Question

The ellipse $\dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{16}=1$ and the hyperbola $\dfrac{{{x}^{2}}}{25}-\dfrac{{{y}^{2}}}{16}=1$, have in common
A. centre only
B. centre, foci and directrices
C. centre, foci and vertices
D. centre and vertices only

Answer 1

We first define the general equation of ellipse and hyperbola and their different parts. We then equate that with the given equations. Using the values, we find out the common characteristics of those two conics.

Complete step by step answer:
We have been given two conics, one of ellipse and one hyperbola.
We first define the general equation of ellipse and its different parts.
General equation of ellipse is $\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1$. The eccentricity of the ellipse is $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$.
The centre will be $\left( \alpha ,\beta \right)$. Coordinates of vertices are $\left( \alpha \pm a,\beta \right)$. Coordinates of foci are $\left( \alpha \pm ae,\beta \right)$. Equations of the directrices are $x=\alpha \pm \dfrac{a}{e}$.
Now for our given equation $\dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{16}=1$. Equating we get $\alpha =0,\beta =0,a=5,b=4$.
The eccentricity of the ellipse is $e=\sqrt{1-\dfrac{{{4}^{2}}}{{{5}^{2}}}}=\dfrac{3}{5}$.
The centre will be $\left( 0,0 \right)$. Coordinates of vertices are $\left( \pm 5,0 \right)$. Coordinates of foci are $\left( \pm 3,0 \right)$. Equations of the directrices are $x=\pm \dfrac{25}{3}$.
We now define the general equation of hyperbola and its different parts.
General equation of ellipse is $\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1$. The eccentricity of the ellipse is $e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$.
The centre will be $\left( \alpha ,\beta \right)$. Coordinates of vertices are $\left( \alpha \pm a,\beta \right)$. Coordinates of foci are $\left( \alpha \pm ae,\beta \right)$. Equations of the directrices are $x=\alpha \pm \dfrac{a}{e}$.
Now for our given equation $\dfrac{{{x}^{2}}}{25}-\dfrac{{{y}^{2}}}{16}=1$. Equating we get $\alpha =0,\beta =0,a=5,b=4$.
The eccentricity of the ellipse is $e=\sqrt{1+\dfrac{{{4}^{2}}}{{{5}^{2}}}}=\dfrac{\sqrt{41}}{5}$.
The centre will be $\left( 0,0 \right)$. Coordinates of vertices are $\left( \pm 5,0 \right)$. Coordinates of foci are $\left( \pm \sqrt{41},0 \right)$. Equations of the directrices are $x=\pm \dfrac{25}{\sqrt{41}}$.

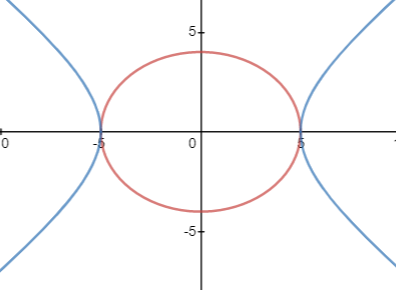
So, we can see for the ellipse $\dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{16}=1$ and the hyperbola $\dfrac{{{x}^{2}}}{25}-\dfrac{{{y}^{2}}}{16}=1$, they have their centre and vertices in common.

So, the correct answer is “Option D”.

Note: The changes happened because of the value of the eccentricity. It has been used in cases of Coordinates of foci and equations of the directrices which are $\left( \alpha \pm ae,\beta \right)$ and $x=\alpha \pm \dfrac{a}{e}$ respectively.