Question

The elevator shown in the figure is descending, with an acceleration of $2\text{ m/}{{\text{s}}^{2}}$. The mass of block A is $0.5kg$. The force exerted by block A on block B is

$\begin{aligned} & \text{A}\text{. }2\text{ N} \\\ & \text{B}\text{. 4 N} \\\ & \text{C}\text{. 6 N} \\\ & \text{D}\text{. 8 N} \\\ \end{aligned}$

Answer 1

Hint: When an object is accelerated, it experiences an apparent force due to the acceleration of the body known as the pseudo force. If we draw the free body diagram of an object we get a good idea of all the forces acting on the body. From that we can find the force acting on B by A.

Complete step by step answer:

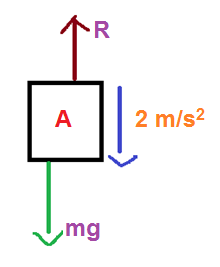
So by drawing the free body diagram of block A, we can see that the pseudo force is acting on the block A acting downwards, we also have the weight of the object acting downwards, the reaction force acting upwards. So if we try to write it down as an equation, we will get
${{F}_{g}}-R={{F}_{a}}$
Where,
${{F}_{g}}$ is the weight acting downwards.
${{F}_{a}}$ is the pseudo force acting on the body
R is the reaction force acting upwards.
We know that the weight of the body is mass times the acceleration due to gravity $\left( g \right)$ and the pseudo force is the mass times the acceleration of the block $\left( a \right)$. So we can write,
$mg-R=ma$
$\Rightarrow R=m(g-a)$
Substituting the values of m, g and a in the above equation, we get
$R=\left( 0.5kg \right)\times \left( 9.8-2 \right)m/{{s}^{2}}$
$\therefore R=3.9\approx 4\text{ N}$
So the reaction force acting upwards is $4\text{ N}$.
According to Newton’s third law, we know that the forces occur in pairs. So the force acting on block B by block A will be equal to the reaction force.
So the force acting on block B by block A is $4\text{ N}$.
So the answer to the question is option (B).

Note:
Newton’s Third Law states that ‘For every reaction, there is an equal and opposite reaction’. These action-reaction forces occur in pairs and act on different objects and not on the same object.
For a person who is inside the box (accelerated frame of reference), will feel that the two boxes are at rest and the whole system including himself is being accelerated upwards with an acceleration of $2m/{{s}^{2}}$.
We can get the same result for the force acting on block B by block A by considering ourselves inside the box as I have mentioned in the above point.