Question
Question: The elevator shown in figure is descending, with an acceleration of \(2m/{s^2}\). The mass of the bl...
The elevator shown in figure is descending, with an acceleration of 2m/s2. The mass of the block A is 0.5 kg. The force exerted by the block A on the block B is -
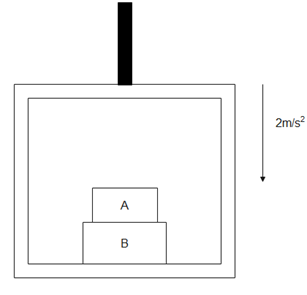
Solution
While we travel in an elevator that goes down we feel that we had lost some weight and when the elevator goes up we feel weight gain. But the actual mass of us is the same in both cases. It's all due to the variation of normal reactions in both the cases. This can be solved from the ground reference frame.
Formula used:
\eqalign{
& mg - N = ma \cr
& N = mg - ma \cr
& N = W - ma \cr}
Complete answer:
When elevator is not moving let the weight of the block be W
W=mg
Where m is the mass of block A and g is the acceleration due to gravity
Now when elevator starts moving down with acceleration ‘a’
Normal reaction N acts upward
Weight W acts downward
Force m×a acts downward
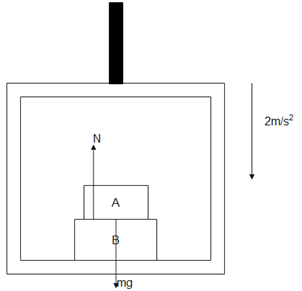
From ground frame of reference
Balancing the forces gives us
\eqalign{
& mg - N = ma \cr
& \Rightarrow N = mg - ma \cr
& \Rightarrow N=W - ma \cr
& \Rightarrow N = 0.5g - 0.5a \cr
& \Rightarrow N = 5 - \left( {0.5 \times 2} \right) \cr
& \therefore N = 5 - 1 = 4Newton \cr}
Hence force exerted by block A on block B is 4 newton.
Additional information:
Same question can be solved by the elevator frame of reference. Here pseudo force comes into action. Since elevator blocks system is moving down with acceleration ‘a’ pseudo force will be acting upward and it will be m×a
Upward forces = N+ma
Downward forces = mg
Equating both the forces we get
N=W−ma
Hence both methods will give us the same answer.
Note:
It is to be noted that only weight seems to be increased but not mass. Because mass is always constant wherever we go but weights vary as resultant acceleration varies. A freely falling body feels no weight due to the same property as resultant acceleration would be (g-g =0)zero. This is called weightlessness. Same applies with the astronaut in the satellite where he feels weightlessness.
