Solveeit Logo
Login

Question

Question: The elevation of the top of a tower from a point on the ground is \(45{}^\circ \) on travelling 60m ...

The elevation of the top of a tower from a point on the ground is 45∘45{}^\circ on travelling 60m from the point towards, the elevation of the top becomes 60∘60{}^\circ . The height of the tower, in meters,
A. 30
B. 30(3−3)30\left( 3-\sqrt{3} \right)
C. 30(3+3)30\left( 3+\sqrt{3} \right)
D. 30330\sqrt{3}

Explanation

Solution

Hint: For the above question we will first draw the diagram for the given condition in the question and then we will use the trigonometric ratios to find the required height of the tower. Since, we know that trigonometric ratios are the relation among the sides and angles of a right angle triangle that is why we are using this. So, here we will use tan⁡θ=perpendicularbase\tan \theta =\dfrac{perpendicular}{base}.

Complete step-by-step answer:
We have been given that the elevation of the top of a tower from a point on the ground is 45∘45{}^\circ on travelling 60m from the point towards, the elevation of the top becomes 60∘60{}^\circ .
Let us suppose the tower AB of height ‘h’ and C and D are the point from where the angles of elevation are 45∘45{}^\circ and 60∘60{}^\circ respectively and the distance between them is 60m.

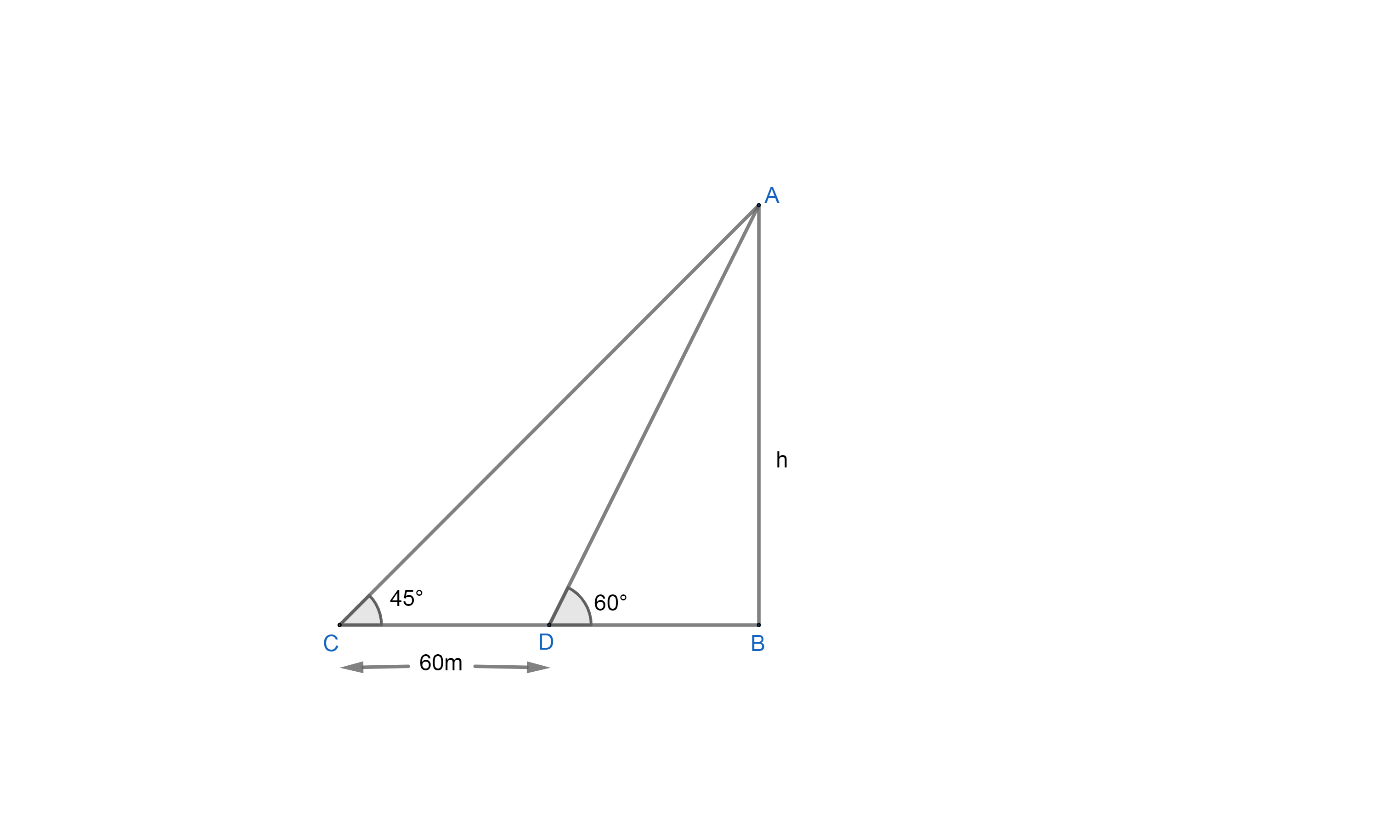
Let us consider ΔABC\Delta ABC,
tan⁡C=ABBC\tan C=\dfrac{AB}{BC}
We have ∠C=45∘,AB=h and BC=BD+CD=(BD+60)\angle C=45{}^\circ ,AB=h\ and\ BC=BD+CD=\left( BD+60 \right)
⇒tan⁡45∘=hBD+60\Rightarrow \tan 45{}^\circ =\dfrac{h}{BD+60}
Since, we know the value of tan⁡45∘=1\tan 45{}^\circ =1.
⇒1=hBD+60 ⇒h=BD+60........(1) \begin{aligned} & \Rightarrow 1=\dfrac{h}{BD+60} \\\ & \Rightarrow h=BD+60........\left( 1 \right) \\\ \end{aligned}
Now, let us consider ΔABD\Delta ABD,
tan⁡D=ABBD\tan D=\dfrac{AB}{BD}
We have AB=h and ∠D=60∘AB=h\ and\,\angle D=60{}^\circ
⇒tan⁡60∘=hBD\Rightarrow \tan 60{}^\circ =\dfrac{h}{BD}
Since, we know that tan⁡60∘=3\tan 60{}^\circ =\sqrt{3}.
⇒3=hBD ⇒h=BD3 ⇒BD=h3........(2) \begin{aligned} & \Rightarrow \sqrt{3}=\dfrac{h}{BD} \\\ & \Rightarrow h=BD\sqrt{3} \\\ & \Rightarrow BD=\dfrac{h}{\sqrt{3}}........\left( 2 \right) \\\ \end{aligned}
Substituting value of BD from equation (2) in equation (1), we get,
h=h3+60 h−h3=60 \begin{aligned} & h=\dfrac{h}{\sqrt{3}}+60 \\\ & h-\dfrac{h}{\sqrt{3}}=60 \\\ \end{aligned}
Taking ‘h’ as common,
h(1−13)=60 h(3−13)=60 h=6033−1 \begin{aligned} & h\left( 1-\dfrac{1}{\sqrt{3}} \right)=60 \\\ & h\left( \dfrac{\sqrt{3}-1}{\sqrt{3}} \right)=60 \\\ & h=\dfrac{60\sqrt{3}}{\sqrt{3}-1} \\\ \end{aligned}
On rationalising the denominator we get,
h=603(3+1)(3−1)(3+1)h=\dfrac{60\sqrt{3}\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}-1 \right)\left( \sqrt{3}+1 \right)}
Using the identity (a+b)(a−b)=a2−b2\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}
⇒h=60(3+3)(3)2−(1)2 =60(3+3)2 ⇒h=30(3+3)m \begin{aligned} & \Rightarrow h=\dfrac{60\left( 3+\sqrt{3} \right)}{{{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}}} \\\ & =\dfrac{60\left( 3+\sqrt{3} \right)}{2} \\\ & \Rightarrow h=30\left( 3+\sqrt{3} \right)m \\\ \end{aligned}
Hence, the height is 30(3+3)meters30\left( 3+\sqrt{3} \right)meters.
Therefore, the correct option is C.

Note: Be careful while doing calculation and solving the equation (1) and (2). Also, take care of the sign during rationalizing the denominator (3−1)\left( \sqrt{3}-1 \right).
Also, remember that in these types of height and distance problems it is necessary that first we should draw the diagram and then we move further to solve it otherwise it is very difficult to analyse the situation of the problem.