Question

The element crystallizes in a body centred cubic lattice and the edge of unit cell is 0.351 nm. The density is 0.533 $\text{g/c}{{\text{m}}^{\text{3}}}$. What is the atomic weight?
(a) 12.0
(b) 6.94
(c) 9.01
(d) 10.8

Answer 1

Answer to this question can be approached by defining a body centred cubic lattice first and then relating packing dfraction, density and mass of a cube which are given by several formulas.

Complete answer:
In the classes of chemistry, we have come across the concepts of physical chemistry and also some part of inorganic chemistry which tells about the arrangements of atoms in a space and their detailed structure such as in the form of primitive cell, unit cells, body centred cubic, face centred cubic etc.
Let us see this concept in detail so that we can derive the correct answer.
This is the structure of a body-centred unit cell-

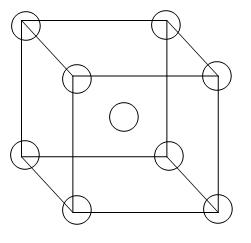
From the diagram we can see that 8 atoms are arranged in all the corners of the cube and there is 1 atom in the centre of the unit cell. Therefore, the contribution per unit cell will be
For primitive – 8 atoms are arranged in all the corners of the cube, therefore, the contribution per unit cell will be 1 atom, $8\text{x}\dfrac{1}{8}=1$ atom or molecule.
Total contribution = 1 atom (primitive) + 1 atom (body centred) = 2
Now, let us write the formula for density of a unit cell.
Density (d) = $\dfrac{\text{Z x M}}{{{\text{a}}^{\text{3}}}\text{ x }{{\text{N}}_{\text{A}}}}$ , where,
Z = atom per unit cell = 2 (in case of Body Centred cubic lattice)
M = Mass / weight (unknown)
a = length of edge = 0.351 nm
${{\text{N}}_{\text{A}}}$= Avogadro’s constant = $\text{6}\text{.022 x 1}{{\text{0}}^{\text{23}}}$
From this formula, we can calculate atomic weight as-
$\text{M = }\dfrac{\text{d x }{{\text{a}}^{\text{3}}}\text{ x }{{\text{N}}_{\text{A}}}}{\text{Z}}$
$\text{M = }\dfrac{\text{0}\text{.533 x (3}\text{.51 x 1}{{\text{0}}^{\text{-8}}}{{\text{)}}^{\text{3}}}\text{ x 6}\text{.022 x 1}{{\text{0}}^{\text{23}}}}{2}$
M = 6.94

Therefore, the answer is – option (b) – the atomic weight of the element is 6.94 g.

Note:
Do not be confused with the body centred and face centred cube where the difference lies only in the part that in BCC there is one additional atom in the centre of each cube and in FCC there is one additional atom in each of the six faces of a cube.