Question
Question: The electrostatic potential V at a point on the circumference of a thin non-conducting disk of radiu...
The electrostatic potential V at a point on the circumference of a thin non-conducting disk of radius r and uniform charge density σ is given by equation V = 4σr. Which of the following expression correctly represents electrostatic energy stored in the electric field of a similar charged disk of radius R?
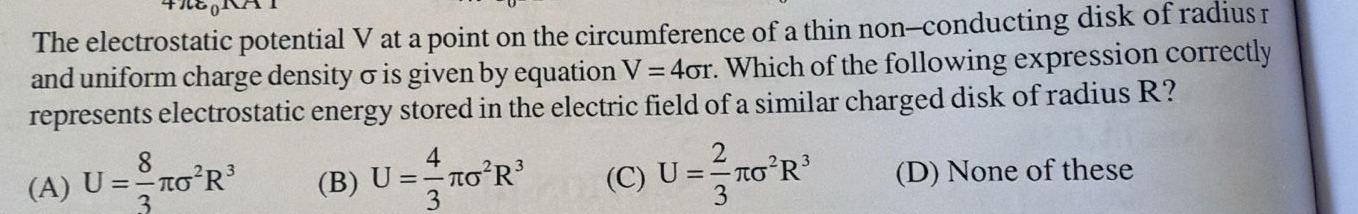
U = 38πσ2R3
U = 34πσ2R3
U = 32πσ2R3
None of these
U = 32πσ2R3
Solution
The electrostatic energy stored in the electric field of a uniformly charged thin non-conducting disk of radius R and uniform charge density σ is given by the standard formula:
U=3ϵ02πσ2R3
Comparing this with the given options, and assuming the options are missing the factor 1/ϵ0, option (C) matches the standard result. The given potential formula for the circumference is likely extraneous or incorrect.
