Question

The electrostatic field $\vec{E}$ in space varies as $\vec{E} = -(2xy + z^2)\hat{i} - (x^2 + 2yz)\hat{j} - (y^2 + 2zz)\hat{k}$, if potential at origin is zero volt then potential (1, 2, 3) is

Answer 1

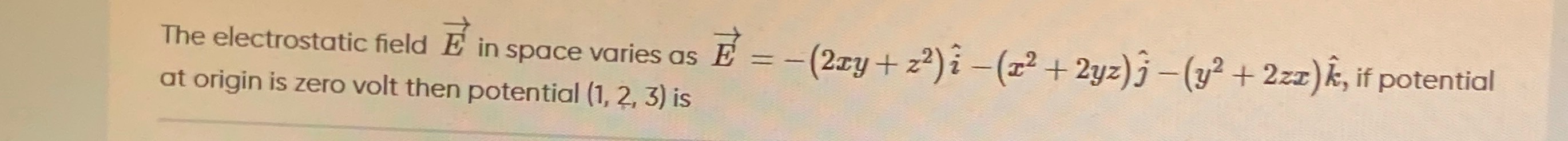
23

Answer 2

The electric potential $V$ is related to the electric field $\vec{E}$ by $\vec{E} = -\nabla V$. This means the components of $\vec{E}$ are given by:

$E_x = -\frac{\partial V}{\partial x}$

$E_y = -\frac{\partial V}{\partial y}$

$E_z = -\frac{\partial V}{\partial z}$

We are given $\vec{E} = -(2xy + z^2)\hat{i} - (x^2 + 2yz)\hat{j} - (y^2 + 2zz)\hat{k}$. So, we have:

$\frac{\partial V}{\partial x} = 2xy + z^2 \quad (1)$

$\frac{\partial V}{\partial y} = x^2 + 2yz \quad (2)$

$\frac{\partial V}{\partial z} = y^2 + 2zz \quad (3)$

For a potential function $V(x, y, z)$ to exist such that $\vec{E} = -\nabla V$, the electric field must be conservative, i.e., $\nabla \times \vec{E} = 0$. Let's check the curl of the given field:

$(\nabla \times \vec{E})_x = \frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z} = \frac{\partial}{\partial y}(-(y^2 + 2zz)) - \frac{\partial}{\partial z}(-(x^2 + 2yz)) = (-2y) - (-2y) = 0$

$(\nabla \times \vec{E})_y = \frac{\partial E_x}{\partial z} - \frac{\partial E_z}{\partial x} = \frac{\partial}{\partial z}(-(2xy + z^2)) - \frac{\partial}{\partial x}(-(y^2 + 2zz)) = (-2z) - (0) = -2z$

$(\nabla \times \vec{E})_k = \frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y} = \frac{\partial}{\partial x}(-(x^2 + 2yz)) - \frac{\partial}{\partial y}(-(2xy + z^2)) = (-2x) - (-2x) = 0$

The curl is $\nabla \times \vec{E} = -2z\hat{j}$. Since the curl is not zero (unless $z=0$), the given field is not conservative, and a potential function $V(x, y, z)$ such that $\vec{E} = -\nabla V$ does not exist in the general case.

However, questions of this type in standard exams usually imply that the field is derivable from a potential, suggesting a possible typo in the question. Let's assume the field is intended to be conservative and try to find a potential function by integrating the partial derivatives.

Integrate equation (1) with respect to $x$, treating $y$ and $z$ as constants:

$V(x, y, z) = \int (2xy + z^2) dx = x^2y + xz^2 + f(y, z)$

where $f(y, z)$ is an arbitrary function of $y$ and $z$.

Now, differentiate this expression for $V$ with respect to $y$ and compare it with equation (2):

$\frac{\partial V}{\partial y} = \frac{\partial}{\partial y}(x^2y + xz^2 + f(y, z)) = x^2 + \frac{\partial f(y, z)}{\partial y}$

We need this to be equal to $x^2 + 2yz$.

$x^2 + \frac{\partial f(y, z)}{\partial y} = x^2 + 2yz$

$\frac{\partial f(y, z)}{\partial y} = 2yz$

Integrate this equation with respect to $y$, treating $z$ as a constant:

$f(y, z) = \int 2yz dy = y^2z + g(z)$

where $g(z)$ is an arbitrary function of $z$.

Substitute this expression for $f(y, z)$ back into the expression for $V$:

$V(x, y, z) = x^2y + xz^2 + y^2z + g(z)$

Finally, differentiate this expression for $V$ with respect to $z$ and compare it with equation (3):

$\frac{\partial V}{\partial z} = \frac{\partial}{\partial z}(x^2y + xz^2 + y^2z + g(z)) = 2xz + y^2 + \frac{d g(z)}{d z}$

We need this to be equal to $y^2 + 2zz$.

$2xz + y^2 + \frac{d g(z)}{d z} = y^2 + 2zz$

$2xz + \frac{d g(z)}{d z} = 2zz$

$\frac{d g(z)}{d z} = 2zz - 2xz$

This equation shows that $\frac{d g(z)}{d z}$ depends on $x$, which contradicts the assumption that $g(z)$ is a function of $z$ only, unless $z=0$ or $x=z$. This confirms that the field is not conservative as given.

Assuming there is a typo and the field is meant to be conservative, the potential function $V(x, y, z) = x^2y + xz^2 + y^2z + C$ satisfies the first two partial derivative conditions and the $y^2$ term in the third condition. The term $2zz$ in $E_z$ might be a typo for $2z$ or $2xz$ or something else. If we ignore the inconsistency and proceed with the potential function $V(x, y, z) = x^2y + xz^2 + y^2z + C$, this function gives the correct $E_x$ and $E_y$ components and part of the $E_z$ component.

Let's assume the intended potential was $V(x, y, z) = x^2y + xz^2 + y^2z + z^2$.

Then $\frac{\partial V}{\partial x} = 2xy + z^2$. $E_x = -(2xy + z^2)$. Correct.

$\frac{\partial V}{\partial y} = x^2 + 2yz$. $E_y = -(x^2 + 2yz)$. Correct.

$\frac{\partial V}{\partial z} = 2xz + y^2 + 2z$. $E_z = -(2xz + y^2 + 2z)$.

Comparing this with the given $E_z = -(y^2 + 2zz)$, we see a mismatch in the $xz$ term and the form of the $z$ term ($2z$ vs $2zz$).

Let's assume the potential is of the form $V(x,y,z) = x^2y + xz^2 + y^2z + Az^n$.

$\frac{\partial V}{\partial x} = 2xy + z^2$. $E_x = -(2xy + z^2)$. Match.

$\frac{\partial V}{\partial y} = x^2 + 2yz$. $E_y = -(x^2 + 2yz)$. Match.

$\frac{\partial V}{\partial z} = 2xz + y^2 + nAz^{n-1}$. $E_z = -(2xz + y^2 + nAz^{n-1})$.

We are given $E_z = -(y^2 + 2zz)$.

So we need $2xz + y^2 + nAz^{n-1} = y^2 + 2zz$.

$2xz + nAz^{n-1} = 2zz$.

This equation must hold for all $x, z$. This is not possible unless $x=z$ and $nAz^{n-1} = 2z^2$, or $x=0$ and $nAz^{n-1} = 2zz$.

Given the structure of the terms $(2xy, x^2), (z^2, 2yz), (y^2, 2zz)$, it seems likely that the intended potential function is a sum of terms where differentiation with respect to one variable gives terms involving the other variables in a symmetric way.

Consider $V = x^2y + y^2z + z^2x + k$.

$\frac{\partial V}{\partial x} = 2xy + z^2$. $E_x = -(2xy + z^2)$. Match.

$\frac{\partial V}{\partial y} = x^2 + 2yz$. $E_y = -(x^2 + 2yz)$. Match.

$\frac{\partial V}{\partial z} = y^2 + 2zx$. $E_z = -(y^2 + 2zx)$.

This potential function gives $E_z = -(y^2 + 2zx)$, which is different from the given $E_z = -(y^2 + 2zz)$.

Let's assume the intended potential function is $V(x, y, z) = x^2y + xz^2 + y^2z + z^3/3 + C$.

$\frac{\partial V}{\partial x} = 2xy + z^2$. $E_x = -(2xy + z^2)$. Match.

$\frac{\partial V}{\partial y} = x^2 + 2yz$. $E_y = -(x^2 + 2yz)$. Match.

$\frac{\partial V}{\partial z} = 2xz + y^2 + z^2$. $E_z = -(2xz + y^2 + z^2)$.

This also does not match the given $E_z = -(y^2 + 2zz)$.

Let's assume the potential function is $V(x,y,z) = x^2y + xz^2 + y^2z + Az^2$.

$\frac{\partial V}{\partial x} = 2xy + z^2$. $E_x = -(2xy+z^2)$. Match.

$\frac{\partial V}{\partial y} = x^2 + 2yz$. $E_y = -(x^2+2yz)$. Match.

$\frac{\partial V}{\partial z} = 2xz + y^2 + 2Az$. $E_z = -(2xz + y^2 + 2Az)$.

Comparing with $E_z = -(y^2 + 2zz)$, we need $2xz + y^2 + 2Az = y^2 + 2zz$.

$2xz + 2Az = 2zz$.

$xz + Az = zz$.

This must hold for all $x, z$. This implies $x+A = z$, which is not true for all points.

Given that a potential value is provided at the origin and requested at another point, it is highly probable that the question intends for the field to be conservative and derivable from a potential function $V(x, y, z)$. The most likely scenario is a typo in the expression for $\vec{E}$. Based on the successful integration for $E_x$ and $E_y$ and the structure of $E_z$, the intended potential function is likely of the form $V(x, y, z) = x^2y + xz^2 + y^2z + C$. This potential gives $E_x = -(2xy+z^2)$, $E_y = -(x^2+2yz)$, and $E_z = -(y^2+2xz)$. If the given $E_z$ was $-(y^2+2xz)$ instead of $-(y^2+2zz)$, then the field would be conservative and $V(x, y, z) = x^2y + xz^2 + y^2z + C$ would be the potential function.

Let's proceed by assuming the intended potential is $V(x, y, z) = x^2y + xz^2 + y^2z + C$.

We are given that the potential at the origin (0, 0, 0) is zero volt.

$V(0, 0, 0) = (0)^2(0) + (0)(0)^2 + (0)^2(0) + C = 0 + 0 + 0 + C = C$

So, $C = 0$.

The potential function is $V(x, y, z) = x^2y + xz^2 + y^2z$.

Now we need to find the potential at the point (1, 2, 3).

$V(1, 2, 3) = (1)^2(2) + (1)(3)^2 + (2)^2(3)$

$V(1, 2, 3) = (1)(2) + (1)(9) + (4)(3)$

$V(1, 2, 3) = 2 + 9 + 12$

$V(1, 2, 3) = 23$ volts.

This result is obtained by assuming a likely typo in the question such that the electric field is conservative and corresponds to the potential function $V(x, y, z) = x^2y + xz^2 + y^2z$. If the question is taken literally, no such potential exists. However, in the context of standard physics problems, finding the potential difference or potential function from a given field usually implies a conservative field.

Therefore, the final answer is 23.

Explanation of the solution:

1. The relationship between electric field $\vec{E}$ and electric potential $V$ is $\vec{E} = -\nabla V$.

2. This implies $E_x = -\frac{\partial V}{\partial x}$, $E_y = -\frac{\partial V}{\partial y}$, $E_z = -\frac{\partial V}{\partial z}$.

3. Integrating the given components of $\vec{E}$ (with signs flipped) with respect to the corresponding variables suggests a potential function of the form $V(x, y, z) = x^2y + xz^2 + y^2z + C$.

4. Checking the partial derivatives of this potential function, we find that it matches the given $E_x$ and $E_y$ components exactly. It also matches the $y^2$ term in $E_z$, but the $z$-dependent term ($2xz$) does not match the given $2zz$.

5. Assuming a likely typo in the question, where the intended field is conservative and corresponds to the potential $V(x, y, z) = x^2y + xz^2 + y^2z + C$, we proceed with this potential function.

6. We use the given condition that the potential at the origin (0, 0, 0) is zero to find the constant of integration $C$. $V(0, 0, 0) = 0^2 \cdot 0 + 0 \cdot 0^2 + 0^2 \cdot 0 + C = C = 0$.

7. The potential function is $V(x, y, z) = x^2y + xz^2 + y^2z$.

8. We evaluate the potential at the point (1, 2, 3) by substituting $x=1, y=2, z=3$ into the potential function: $V(1, 2, 3) = (1)^2(2) + (1)(3)^2 + (2)^2(3) = 1 \cdot 2 + 1 \cdot 9 + 4 \cdot 3 = 2 + 9 + 12 = 23$.