Question
Question: The electrical potential function for an electric field directed parallel to the x-axis is shown in ...
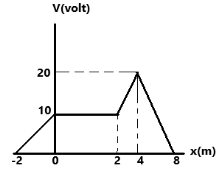
The electrical potential function for an electric field directed parallel to the x-axis is shown in Fig. The graph Ex versus x will be-
(A) 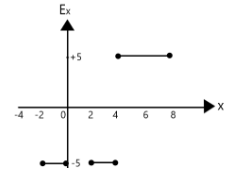
(B) 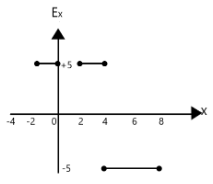
(C) 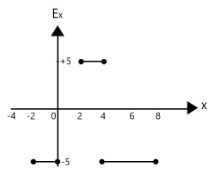
(D) 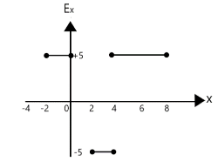
Solution
The Electric field can also be defined as the gradient of potential which is the slope of a potential graph. The increase in potential gives a negative Electric field while the decrease in potential corresponds to a positive Electric field. So using this information we can find the graph for the electric field.
Formula used: In this solution we will be using the following formula;
Ex=−ΔxΔV where Ex is the electric field along x axis, ΔV is the change in potential along the same axis, and Δx is the change in distance in the x axis.
Complete Step-by-Step Solution
In electrostatics, the electric field created by a charge can be regarded as the rate of change of the electric potential with distance, that is to say how fast the potential changes as we move away from the charge. Mathematically, it can be expressed as
Ex=−ΔxΔV where ΔV is the change in potential along the same axis, and Δx is the change in distance in the x -axis. The negative sign implies that a positive gradient implies a negative electric field, i.e. if electric potential increases as we increase distance then electric field is negative, likewise, if it decreases with distance then electric field is positive.
We shall calculate the slope of the graph at every stop (joint in graph).
From x=−2 to x=0 ,
Ex=−ΔxΔV=−0−(−2)(10−0)=−210=−5
Ex=−5N/C . Thus we can eliminate option B and D.
From x=0 to x=2 , we see that there is no change in potential. Thus ΔV=0 . So there is also no change in the electric field.
From x=2 to x=4
Ex=ΔxΔV=−4−220−10=−5 . Hence, we can eliminate option C.
Hence option A is our answer.
Note
Alternatively, without going through lengthy calculations, we can say that since a positive slope corresponds to a negative Electric field, then:
From x=−2 to x=0 Electric field must be negative (a line moving upward from right to left is a positive slope), which eliminates B and D.
Similarly, from x=2 to x=4 also has a positive slope, hence Electric field must be negative too. This eliminates option C, and leaves us with A as our answer.
