Question

The electric potential (in volt) in a region along the x-axis varies with x according to the relation $V(x) = 5 + 4x^2$, where x is in m. Therefore, force experienced by a charge of 1C placed at x = -1m is ____ N.

Answer 1

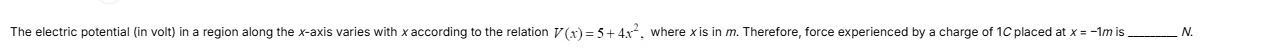
8

Answer 2

The electric potential along the x-axis is given by $V(x) = 5 + 4x^2$.

The electric field component along the x-axis, $E_x$, is related to the potential gradient by the formula $E_x = -\frac{dV}{dx}$.

Differentiating $V(x)$ with respect to x: $\frac{dV}{dx} = \frac{d}{dx}(5 + 4x^2) = 0 + 4(2x) = 8x$.

So, the electric field along the x-axis is $E_x(x) = -8x$.

We need to find the force experienced by a charge of $q = 1C$ placed at $x = -1m$.

First, let's find the electric field at $x = -1m$: $E_x(-1) = -8(-1) = 8$ V/m.

The force experienced by a charge q in an electric field $\vec{E}$ is given by $\vec{F} = q\vec{E}$. Since the field is only along the x-axis, the force is also only along the x-axis, $F_x = qE_x$.

Given the charge $q = 1C$ and the electric field at $x = -1m$ is $E_x(-1) = 8$ V/m: $F_x = (1C) \times (8 V/m) = 8$ N.

The force experienced by the charge is 8 N in the positive x-direction. The magnitude of the force is 8 N.