Solveeit Logo
Login

Question

Question: The electric potential function for an electric field directed parallel to the X-axis is shown in fi...

The electric potential function for an electric field directed parallel to the X-axis is shown in figure. The intervals in which the magnitude of the electric field in the X-axis direction is maximum are,


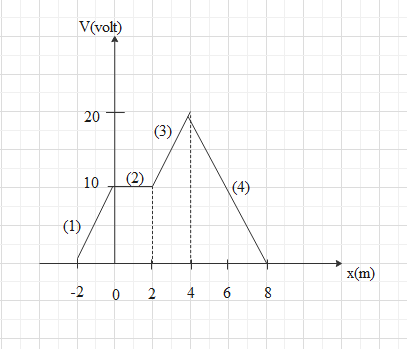
(A) −2≤x≤0,4≤x≤8,and0≤x≤2-2\le x\le 0,4\le x\le 8,and0\le x\le 2
(B) −2≤x≤0,and0≤x≤2-2\le x\le 0,and0\le x\le 2
(C) −2≤x≤0,2≤x≤4and4≤x≤8-2\le x\le 0,2\le x\le 4and4\le x\le 8
(D) 0≤x≤2,and4≤x≤80\le x\le 2,and4\le x\le 8

Explanation

Solution

The graph of electric potential function for an electric field directed parallel to the X-axis is given and the graph of the magnitude of the electric field in the X-axis direction has to be found. The graph of the magnitude of the electric field in the X-axis direction has positive and negative values of the electric field, so the maximum magnitude of the electric field is the maximum electric field.
Formula used:
E=−dvdxE=-\dfrac{dv}{dx}

Complete answer:
In the question the graph of the electric potential function for an electric field directed parallel to the X-axis is given. From the relation between electric field and electric potential the graph of the intervals in which the magnitude of the electric field in the X-axis direction can be converted. The slope of the above graph is an electric field parallel to the X-axis.

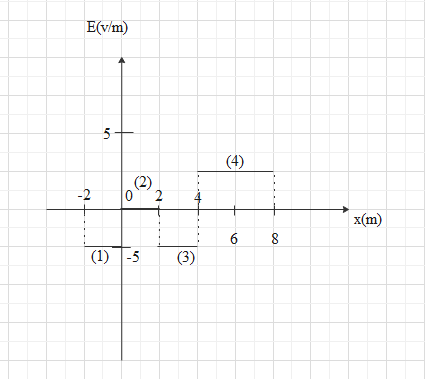
So, for the part(1)(1): E=−10−00−(−2)=−5E=-\dfrac{10-0}{0-(-2)}=-5
∴E=∣−5∣=5\therefore E=\left| -5 \right|=5
For the part(2)(2): E=−02−0=0E=-\dfrac{0}{2-0}=0
∴E=∣0∣=0\therefore E=\left| 0 \right|=0
For the part(3)(3): E=−20−104−2=−5E=-\dfrac{20-10}{4-2}=-5
∴E=∣−5∣=5\therefore E=\left| -5 \right|=5
For the part(4)(4): E=−20−04−8=5E=-\dfrac{20-0}{4-8}=5
∴E=∣5∣=5\therefore E=\left| 5 \right|=5

So the range of the intervals in which the magnitude of the electric field in the X-axis direction is maximum are:

−2≤x≤0-2\le x\le 0
2≤x≤42\le x\le 4
4≤x≤84\le x\le 8.

So, the correct answer is “Option C”.

Additional Information:
The line integral of the eclectic field between point P and Q is the voltage difference between that two points and vice versa if the distance between two point is very small then dv→ =−E→ ⋅dl→ \overset{\to }{\mathop{dv}}\,=-\overset{\to }{\mathop{E}}\,\cdot \overset{\to }{\mathop{dl}}\,. So, E=−dvdxE=-\dfrac{dv}{dx}.

Note:
If the electric field is negative it only says that the direction of the field is convergent and if the field is positive it only says that the field is divergent. In both the case if the magnitude of the electric field is the same, the intensities of both are the same.