Solveeit Logo
Login

Question

Question: The electric potential due to infinite uniformly charge of linear charge density \(\lambda \) at a d...

The electric potential due to infinite uniformly charge of linear charge density λ\lambda at a distance r from is given by is the reference point ro{{r}_{o}}
a)2 !!λ!! 4 !!π!! ∈or b)2 !!λ!! 4 !!π!! ∈or0 c)2 !!λ!! [ln⁡ro−ln⁡r]4 !!π!! ∈o d)2 !!λ!! (lnr)4 !!π!! ∈or \begin{aligned} & a)\dfrac{\text{2 }\\!\\!\lambda\\!\\!\text{ }}{\text{4 }\\!\\!\pi\\!\\!\text{ }{{\in }_{\text{o}}}r} \\\ & b)\dfrac{\text{2 }\\!\\!\lambda\\!\\!\text{ }}{\text{4 }\\!\\!\pi\\!\\!\text{ }{{\in }_{\text{o}}}{{r}_{0}}} \\\ & c)\dfrac{\text{2 }\\!\\!\lambda\\!\\!\text{ }\left[ \ln {{r}_{o}}-\ln r \right]}{\text{4 }\\!\\!\pi\\!\\!\text{ }{{\in }_{\text{o}}}} \\\ & d)\dfrac{\text{2 }\\!\\!\lambda\\!\\!\text{ (lnr)}}{\text{4 }\\!\\!\pi\\!\\!\text{ }{{\in }_{\text{o}}}r} \\\ \end{aligned}

Explanation

Solution

The electric field due to an infinitely charge distribution is given by, λ2π∈∘r\dfrac{\lambda }{2\pi {{\in }_{\circ }}r} where λ\lambda is the linear charge density, ∈∘{{\in }_{\circ }} is the permittivity of free space and r is the perpendicular distance from the charge distribution. Hence taking ro{{r}_{o}} as the reference point, the potential at the point which is at a distance r from the charge distribution from the expression i.e. dVdr=Vr−Vrodr=−E...(1)\dfrac{dV}{dr}=\dfrac{{{V}_{r}}-{{V}_{{{r}_{o}}}}}{dr}=-E...(1) where Vr{{V}_{r}} is the potential at point r, Vro{{V}_{{{r}_{o}}}} is the potential at the reference point and E is the electric field at point r.

Complete step-by-step answer:

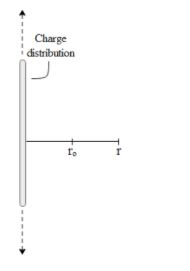
In the above figure we can see a charge distribution of linear charge density λ\lambda . Now we wish to calculate the potential at point r from the linear charge distribution. For that let us use equation 1 to determine the potential at point r with respect to the reference point ro{{r}_{o}}. Let us assume the distance between them is very small i.e. dr.
Vr−Vrodr=−E,since E=λ2π∈∘r Vr−Vro=−λ2π∈∘rdr \begin{aligned} & \dfrac{{{V}_{r}}-{{V}_{{{r}_{o}}}}}{dr}=-E,\text{since }E=\dfrac{\lambda }{2\pi {{\in }_{\circ }}r} \\\ & {{V}_{r}}-{{V}_{{{r}_{o}}}}=-\dfrac{\lambda }{2\pi {{\in }_{\circ }}r}dr \\\ \end{aligned}
Now let us integrate the above equation to find the potential at point r with respect to ro{{r}_{o}}.
Vr−Vro=−∫rorλ2π∈∘rdr Vr−Vro=−λ2π∈∘∫ror1∘rdr Vr−Vro=−λ2π∈∘[ln⁡r]ror Vr−Vro=−λ2π∈∘[ln⁡r−ln⁡ro] Vr−Vro=λ2π∈∘[ln⁡ro−ln⁡r] \begin{aligned} & {{V}_{r}}-{{V}_{{{r}_{o}}}}=-\int\limits_{{{r}_{o}}}^{r}{\dfrac{\lambda }{2\pi {{\in }_{\circ }}r}dr} \\\ & {{V}_{r}}-{{V}_{{{r}_{o}}}}=-\dfrac{\lambda }{2\pi {{\in }_{\circ }}}\int\limits_{{{r}_{o}}}^{r}{\dfrac{1}{_{\circ }r}dr} \\\ & {{V}_{r}}-{{V}_{{{r}_{o}}}}=-\dfrac{\lambda }{2\pi {{\in }_{\circ }}}\left[ \ln r \right]_{{{r}_{o}}}^{r} \\\ & {{V}_{r}}-{{V}_{{{r}_{o}}}}=-\dfrac{\lambda }{2\pi {{\in }_{\circ }}}\left[ \ln r-\ln {{r}_{o}} \right] \\\ & {{V}_{r}}-{{V}_{{{r}_{o}}}}=\dfrac{\lambda }{2\pi {{\in }_{\circ }}}\left[ \ln {{r}_{o}}-\ln r \right] \\\ \end{aligned}
Hence from the above obtained result we can conclude that the potential at point r with respect to the reference point is given by,λ2π∈∘[ln⁡ro−ln⁡r]\dfrac{\lambda }{2\pi {{\in }_{\circ }}}\left[ \ln {{r}_{o}}-\ln r \right] .

So, the correct answer is “Option C”.

Note: If we consider the above equation the potential keeps on decreasing as we move away from the reference point ro{{r}_{o}}. Hence we always take the electric field as a negative gradient of potential between the two points. The potential at a point always varies inversely with the distance.