Question

The electric intensity outside a charged sphere of radius R at a distance r (r > R)

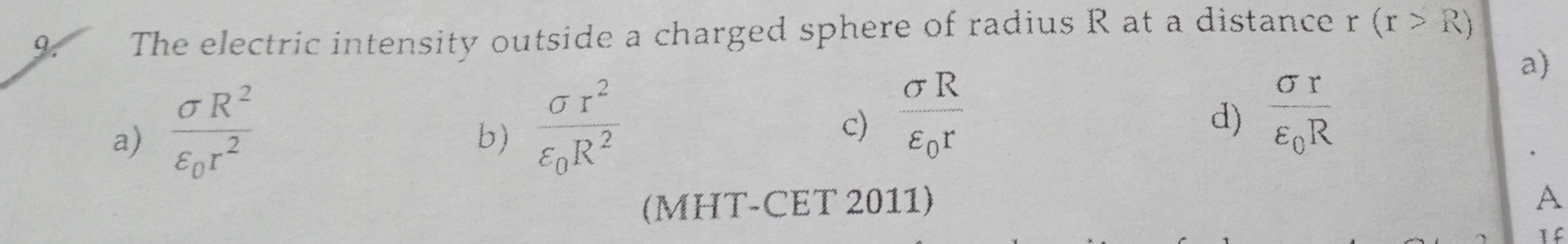
• A. $\frac{\sigma R^2}{\epsilon_0 r^2}$
• B. $\frac{\sigma r^2}{\epsilon_0 R^2}$
• C. $\frac{\sigma R}{\epsilon_0 r}$
• D. $\frac{\sigma r}{\epsilon_0 R}$

Answer 1

Answer: (A)

$\frac{\sigma R^2}{\epsilon_0 r^2}$

Answer 2

For a uniformly charged sphere with surface charge density $\sigma$ and radius $R$, the total charge is:

$Q = \sigma \times 4\pi R^2$.

Using Gauss's law for a spherical Gaussian surface of radius $r > R$:

$E \times 4\pi r^2 = \frac{Q}{\epsilon_0}$.

Substitute $Q$:

$E \times 4\pi r^2 = \frac{\sigma \cdot 4\pi R^2}{\epsilon_0} \Rightarrow E = \frac{\sigma R^2}{\epsilon_0 r^2}$.