Question

The electric intensity due to a dipole of length $10\,{\text{cm}}$ and having a charge of $500\,\mu {\text{C}}$ , at a point on the axis at a distance $20\,{\text{cm}}$ from one of the charges in air, is
A. $6.25 \times {10^7}\,{\text{N}}/{\text{C}}$
B. $9.28 \times {10^7}\,{\text{N}}/{\text{C}}$
C. $13.1 \times {10^{11}}\,{\text{N}}/{\text{C}}$
D. $20.5 \times {10^7}\,{\text{N}}/{\text{C}}$

Answer 1

First of all, we will find the distance between two dipoles followed by distance between the center of dipole and the point. After that we will find the electric dipole moment. After that we will substitute the required values in the expression and manipulate accordingly to obtain the answer.

Formula used:
Electric field by axis due to dipole formula,
$E = \dfrac{{K \times 2pr}}{{{{\left( {{r^2} - {l^2}} \right)}^2}}}$ …… (1)
Where,
$p$ is electric dipole moment
$r$ is distance between the center of dipole and the point
$l$ is the length between center and a dipole.

Complete step by step answer:
From the question we know that,

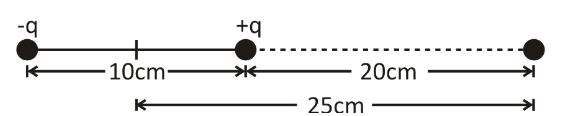
Given,
Electric charge is, $q = 500\,\mu {\text{C}}$
Distance between two dipoles,
d = 10\,{\text{cm}} \\\ \Rightarrow {\text{d}} = 10 \times {10^{ - 2}}\,{\text{m}} \\\ \Rightarrow {\text{d}} = 0.10\,{\text{m}} \\\
Distance between the center of dipole and the point is,
r = 20\,{\text{cm}} \\\ \Rightarrow r = \left( {20 + 5} \right)\,{\text{cm}} \\\ \Rightarrow r = 25\,{\text{cm}} \\\ \Rightarrow r = 0.25\,{\text{m}} \\\
Length,
l = 5\,{\text{cm}} \\\ \Rightarrow l = 5 \times {10^{ - 2}}\,{\text{m}} \\\ \Rightarrow l = 0.05\,{\text{m}} \\\
And, electric dipole moment is,
$p = q \times d \\\ \Rightarrow p = 500 \times {10^{ - 6}} \times 0.1 \\\ \Rightarrow p = 500 \times {10^{ - 7}} \\\ \Rightarrow p = 5 \times {10^{ - 5}}$
We know that, $k = 9 \times {10^9}$

So, put all the value in the formula and we get,
$E = \dfrac{{K \times 2pr}}{{{{\left( {{r^2} - {l^2}} \right)}^2}}} \\\ \Rightarrow E = \dfrac{{9 \times {{10}^9} \times 2 \times \left( {5 \times {{10}^{ - 5}} \times 0.25} \right)}}{{{{\left[ {{{\left( {0.25} \right)}^2} - {{\left( {0.05} \right)}^2}} \right]}^2}}} \\\ \Rightarrow E = \dfrac{{225 \times {{10}^3}}}{{0.0036}} \\\ \therefore E = 6.25 \times {10^7}\,{\text{N}}/{\text{C}}$
Hence, the required answer is $6.25 \times {10^7}\,{\text{N}}/{\text{C}}$ .

The correct option is A.

Additional information:
Electric Field Intensity: As the electric field, the area around an electric charge in which its effect can be felt is defined. At a point, the electric field strength is the force encountered by a positive unit charge imposed at that stage.
Electric field: The electric field per unit charge is known as the electric force. The field’s position is taken to be the direction of the force on a positive test charge that it will exert. From a positive charge, the electric field is radially outward and radially inward towards a negative point charge.

Note: Remember that, because of another charge, as a charge may feel force, the effect here becomes the force, so. E.F may also be referred to as a force field. In this case, electric field intensity, mathematically, which is force experienced through a test charge imposed at that point of the field gives the field strength estimate at that point.