Question

The electric field intensity due to a uniformly charged sphere is zero?
(a). At the centre
(b). At the infinity
(c). At the center and at infinity distance
(d). On the surface

Answer 1

- Hint: To find where the electric field intensity inside due to uniformly charged sphere is zero, we will find the electric field intensity at the centre, at the infinity and on the surface using Gauss’s theorem which can be expressed mathematically as,
$\oint\limits_{s}{\overset{\to }{\mathop{E}}\,\cdot d\overset{\to }{\mathop{s}}\,}=\oint\limits_{s}{\overset{\to }{\mathop{E}}\,\cdot \widehat{n}d\overset{\to }{\mathop{s}}\,=\dfrac{q}{{{\varepsilon }_{0}}}}$.

Formula used: $\oint\limits_{s}{\overset{\to }{\mathop{E}}\,\cdot d\overset{\to }{\mathop{s}}\,}=\oint\limits_{s}{\overset{\to }{\mathop{E}}\,\cdot \widehat{n}d\overset{\to }{\mathop{s}}\,=\dfrac{q}{{{\varepsilon }_{0}}}}$

Complete step-by-step solution -
Now, in the question we are asked to find where the electric field intensity will be zero in a uniformly charged sphere, so, before finding it we will find the electric field intensity of the sphere at any point outside the sphere.
Let $\sigma$ the uniform surface charge density of a sphere of radius R. Now, consider a point P outside the sphere at any place, now to find the electric field intensity we will use the Gauss’s theorem which can be given as,
$\oint\limits_{s}{\overset{\to }{\mathop{E}}\,\cdot d\overset{\to }{\mathop{s}}\,}=\oint\limits_{s}{\overset{\to }{\mathop{E}}\,\cdot \widehat{n}d\overset{\to }{\mathop{s}}\,=\dfrac{q}{{{\varepsilon }_{0}}}}$
Or $\overset{\to }{\mathop{E}}\,\oint\limits_{s}{d\overset{\to }{\mathop{s}}\,}=\dfrac{q}{{{\varepsilon }_{0}}}$ ……………(i)
Where, E is intensity of electric field, q is charge of electric field, s is surface of the sphere.

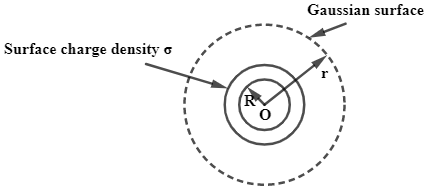
Here, as the charge is uniformly distributed in the sphere, we will consider s as an area of the sphere which is, $s=4\pi {{r}^{2}}$ and r is radius of the gaussian surface shown in the figure above.
Now, by integrating we will find the intensity of electric field at point p,
$\Rightarrow E\left[ s \right]_{0}^{s}=\dfrac{q}{{{\varepsilon }_{0}}}$
$\Rightarrow E\left[ s-0 \right]=\dfrac{q}{{{\varepsilon }_{0}}}$ ………….(i)
Now, we will substitute the values of s in the expression (i) and we will get,
$\Rightarrow E\left( 4\pi {{r}^{2}} \right)=\dfrac{q}{{{\varepsilon }_{0}}}$
$\Rightarrow E=\dfrac{q}{4\pi {{r}^{2}}{{\varepsilon }_{0}}}$
From this, it can be seen that at point P the electric field intensity is maximum.
Now, we will find the electric field at the surface of sphere, for this we will have $r=R$
So, we will substitute the value of r in expression (i) we will get,
$E=\dfrac{q}{4\pi {{R}^{2}}{{\varepsilon }_{0}}}$
Now, if $\sigma$ is the charge density on the shell, then
$q=4\pi {{R}^{2}}\cdot \sigma$
$\therefore E=\dfrac{4\pi {{R}^{2}}\cdot \sigma }{4\pi {{R}^{2}}{{\varepsilon }_{0}}}=\dfrac{\sigma }{{{\varepsilon }_{0}}}$
From this it can be said that at the surface of the sphere also the intensity is high.
Now, we will calculate the electric field intensity inside the sphere or at centre.

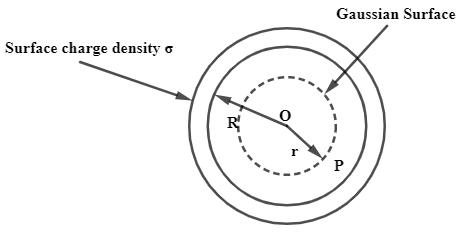
As the charge inside the sphere is zero the electric field intensity can be given by,
$E=\dfrac{0}{4\pi {{R}^{2}}{{\varepsilon }_{0}}}=0$
So, the intensity is zero.
Hence, the electric field intensity inside the sphere is zero.

Thus, option (a) is correct.

Note: In such a question the student might use the direct formula of electric field intensity instead of deriving everything. Here, it was given that the electric field is uniform, now if the field is non uniform, then the solution changes. So, students must read questions carefully before solving it.