Question

The electric field intensity at all points in space is given by $\vec{E} = \sqrt{3}\hat{i} - \hat{j}$ volts/metre. The nature of equipotential lines in x-y plane is given by :-

• A.
• B.
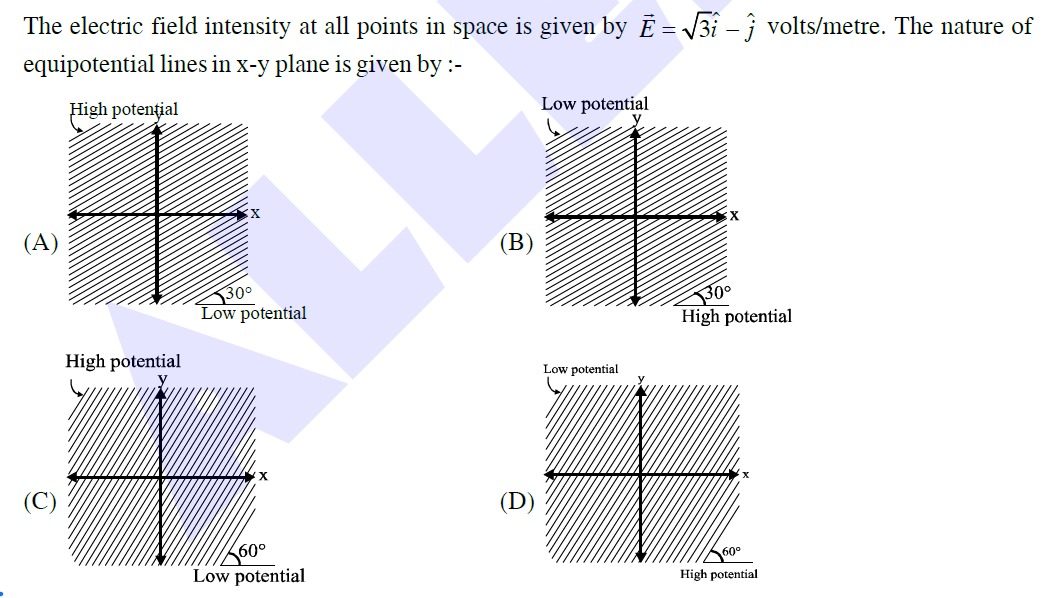
• C.
• D.

Answer 1

Answer: (C)

C

Answer 2

The electric field is given by $\vec{E} = \sqrt{3}\hat{i} - \hat{j}$. Equipotential lines are perpendicular to the electric field lines.

The slope of the electric field vector is $m_E = \frac{-1}{\sqrt{3}}$.

The slope of the equipotential lines is $m_{eq} = -\frac{1}{m_E} = -\frac{1}{(-1/\sqrt{3})} = \sqrt{3}$.

The angle $\theta$ made by the equipotential lines with the positive x-axis is given by $\tan \theta = \sqrt{3}$, so $\theta = 60^\circ$.

The electric field points in the direction of decreasing potential. The direction of $\vec{E}$ is given by the vector $(\sqrt{3}, -1)$, which is in the fourth quadrant, pointing towards the bottom right.

Thus, potential decreases as we move towards the bottom right.

Equipotential lines are given by $y = \sqrt{3}x + k$. For a given x, increasing y increases the potential $V = y - \sqrt{3}x + C$. So, lines with larger y-intercept (or larger y for a given x) have higher potential.

Lines with slope $\sqrt{3}$ and larger y-intercept are located more towards the top left.

Therefore, the top left region has higher potential and the bottom right region has lower potential.

Option (C) shows lines with slope corresponding to $60^\circ$ and indicates high potential in the top left and low potential in the bottom right.