Question
Question: The electric field due to a uniformly charged non-conducting sphere of radius R as a function of the...
The electric field due to a uniformly charged non-conducting sphere of radius R as a function of the distance from its centre is represented graphically by
(A)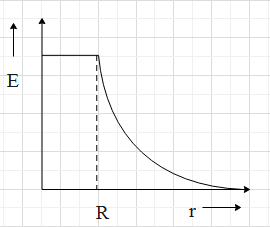
(B)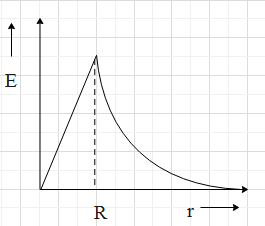
(C)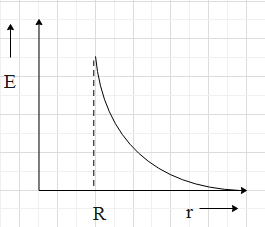
(D)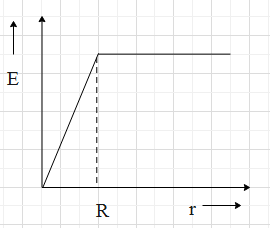
Solution
Hint
The question is based on the properties of the electric field in a sphere. The electric field due to any body is directly proportional to the distance from the radius of the body. The electric field will be maximum at distance equal to the radius length and is inversely proportional to the distance for a length more than that of the radius of the sphere.
⇒E=4πε01r2Q
where E is the electric field,
Q is the charge on the body
r is the distance from the center of the body and εo is the permittivity in free space.
Complete step by step answer
The relation between the electric field and the radius of the sphere for a uniformly charged non-conducting sphere is given as follows.
⇒E=4πε01r2Q
The electric field inside the sphere will be zero. Thus, the charge enclosed by the closed figure that is, a sphere will also be zero. The charges get uniformly accumulated over the surface of the sphere, that is, at a distance from the centre equal to that of the radius of the sphere. Using the formula above, we see that the electric field is inversely proportional to the square of the radius of the sphere. That is,
⇒E∝R21

Let us consider the graph above while going through the explanation.
So, for the distance from the centre to the radius R, the electric field increases, as the distance increases from 0 to the distance equal to R.
This is because, within the sphere, as the radius increases, the amount of charge contained also increases, since the charge is uniformly distributed.
⇒E∝r
At a distance equal to the radius of the sphere, the electric field will be maximum, as, at a distance equal to the radius of the sphere, the electric charges accumulate on the surface of the sphere.
As the distance increases more than R, that is, at a distance away from the sphere, the electric field decreases at a rate of the inverse of the square of the radius of the sphere. Because
⇒E∝r21
∴ The graph B is correct, thus, option (B) is correct.
Note
For the uniformly charged non-conducting sphere, the charge contained per unit volume of the sphere is given by,
⇒ρ=34πR3Q
So the charge contained in a smaller sphere of radius r is given as,
⇒Q′=34πR3Q×34πr3
On cancelling common terms we get,
⇒Q′=R3Qr3
Hence the electric field will be,
⇒E=4πε01r2R3Qr3
On cancelling the r2,
⇒E=4πε01R3Qr
We can see that E∝r.
