Question

The electric field due to a uniformly charged disc at a point very close from the surface of the disc is given by, ($\text{ }\\!\\!\sigma\\!\\!\text{ }$ is the surface charge density of the disc)
A. $E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}$
B. $E=\dfrac{\sigma }{{{\varepsilon }_{0}}}$
C. $E=\dfrac{2\sigma }{{{\varepsilon }_{0}}}$
D. $E=\dfrac{\sigma }{4{{\varepsilon }_{0}}}$

Answer 1

Hint : Suppose if a circular disc has a surface charge density, it will produce an electric field along the axis. The field strength varies as we go from the surface to a point in the axis.

Complete step by step answer:

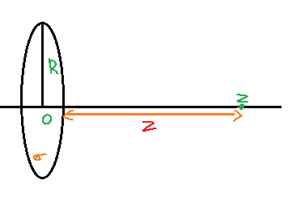
Suppose a circular disc of radius R and has a surface charge density of $\text{ }\\!\\!\sigma\\!\\!\text{ }$, then the electric field at a point on the axis at a distance z from the disc is given by,
$E=k\sigma 2\pi \left[ 1-\dfrac{z}{\sqrt{{{z}^{2}}+{{R}^{2}}}} \right]$
Where, k is the coulomb’s constant, whose value is given by $\dfrac{1}{4\pi {{\varepsilon }_{0}}}$.
If the charge density is considered to be positive, the field will be along the axis directed away from the disc.
So if the point z is very close to the disc, such that z<$E=k\sigma 2\pi \left[ 1-\dfrac{1}{\sqrt{1+\dfrac{{{R}^{2}}}{{{z}^{2}}}}} \right]$
Since the ratio $\dfrac{{{R}^{2}}}{{{z}^{2}}}>>1$ is very much greater than 1, then we can write $\left( 1+\dfrac{{{R}^{2}}}{{{z}^{2}}} \right)$ as $\dfrac{{{R}^{2}}}{{{z}^{2}}}$. The reciprocal of this term will be less than 1 and can be neglected.
So the electric field of the disc at point z after the above approximation can be written as,
$E=k\sigma 2\pi \left[ 1-\dfrac{{{z}^{2}}}{{{R}^{2}}} \right]=k\sigma 2\pi$
Since the ratio, $\dfrac{{{z}^{2}}}{{{R}^{2}}}$ is very less and close to zero, thus neglected.
$E=\dfrac{\sigma 2\pi }{4\pi {{\varepsilon }_{0}}}$
$\therefore E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}$
Therefore, the answer to the question is option (A)- $E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}$
Note :
The electric field produced by a uniform disc of surface charge density $\left( \sigma \right)$ at a distance very far away from the disc behaves like an electric field produced by a point charge. $E=\dfrac{Q}{4\pi {{\varepsilon }_{0}}{{z}^{2}}}$, z is the distance on the axis which is very far away from the disc.
The electric field of a disc of charge can be found by superposing the point charge fields of infinitesimal charge elements. It can be facilitated by summing the fields of charged rings.