Question

The electric field at a distance r outside the conductor is:

& \text{A) }\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{b}}}{{{r}^{2}}} \\\ & \text{B) Zero} \\\ & \text{C) }\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{a}}+{{q}_{b}}}{{{r}^{2}}} \\\ & \text{D) }\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{a}}}{{{r}^{2}}} \\\ \end{aligned}$$

Answer 1

We need to find the electrostatic field developed due to the given spherical shell with cavities inside it. There are two positive charges inside the shell which can contribute to the net electric field produced by the spherical shell of radius ‘R’.

Complete answer:
We are given a spherical shell which has two positive charges in it. Let us consider the radius of the sphere to be the ‘R’. We know that the electric field outside at a distance ‘r’ formed due to charge inside a closed surface is independent of the charge distribution inside the shell. The electric field at any point outside is indirectly proportional to the distance from the centre of the shell.

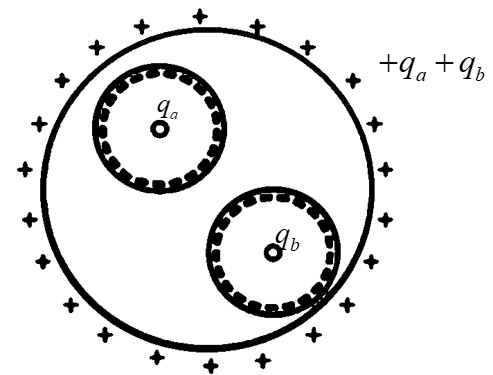
Using the Coulomb’s law of electrostatic force, we can derive the electric field due to the shell as –
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{{{r}^{2}}}$
Now, let us consider our situation. The electric field at a point ‘r’ distance away from the centre of the shell due to the positive charges ${{q}_{a}}\text{ and }{{q}_{b}}$ can be given as –
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{a}}+{{q}_{b}}}{{{r}^{2}}}$
From the above equation, we can understand that the electric field due to the spherical shell with charges ${{q}_{a}}\text{ and }{{q}_{b}}$ at a point outside the shell is
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{a}}+{{q}_{b}}}{{{r}^{2}}}$
This is the required solution for the question given.

So, the correct answer is “Option C”.

Note:
The electric field due to spherical shells with a charge inside is considered equally as point charge. We can find the electric field directly without much complex calculations given that the sphere has a uniform charge density. This is applicable only for those points outside the sphere.