Question

The electric dipole is placed along the x-axis at the origin OF. A point P is at a distance of $20{\text{ cm}}$ from this origin such that OP makes an angle $60^\circ$ with the x - axis. If the electric field at P makes an angle $\theta$ with the x - axis, the value of $\theta$ would be
A. $\dfrac{\pi }{3}$
B. ${\tan ^{ - 1}}\dfrac{{\sqrt 3 }}{2}$
C. $\dfrac{{2\pi }}{3}$
D. $\dfrac{\pi }{3} + {\tan ^{ - 1}}\dfrac{{\sqrt 3 }}{2}$

Answer 1

**Hint: **Resolve the electrical dipole and electric field in two components. Then find the electric field due to the dipole at the axial and equatorial point.
The electric field due to a dipole at an axial point is given by ${E_{axial}} = \dfrac{{2kp}}{{{r^3}}}$ in the direction of the dipole.
The electric field due to a dipole at an equatorial point is given by ${E_{eq}} = \dfrac{{kp}}{{{r^3}}}$ in the direction opposite to that of the dipole.
Here, $p$ is the dipole moment, $r$ is the distance of the point from the dipole and $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$
.
Complete step by step answer
Let us first discuss an electric dipole. It is basically an electrostatic system of two equal and opposite point charges separated by a very small distance.
As given in the question that the electric dipole is placed along the x-axis at the origin O and a point P is at a distance of $20{\text{ cm}}$ from this origin such that OP makes an angle $60^\circ$ with the x - axis. Now, if the electric field at P makes an angle $\theta$ with the x - axis, we have to calculate the value of $\theta$ .
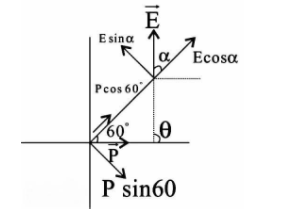
A diagram is given which shows the case.
Let $E$ be the magnitude of the electric field, $\alpha$ be the angle between the electric field and line OP and $r = 20cm$ be the distance OP.
Now, the electric dipole and the electric field vector are resolved into the two components.
We know that the electric field due to a dipole at an axial point is given by ${E_{axial}} = \dfrac{{2kp}}{{{r^3}}}$ in the direction of the dipole.
For the axial point, the dipole moment has value $p\cos 60^\circ$ and the electric field component is $E\cos \alpha$ .
Therefore, according to the above expression we have

$E\cos \alpha = \dfrac{{2kp\cos 60^\circ }}{{{r^3}}}$ …..(i)
We also know that the electric field due to a dipole at an equatorial point is given by ${E_{eq}} = \dfrac{{kp}}{{{r^3}}}$ in the direction opposite to that of the dipole.
For the equatorial point, the dipole moment has value $p\sin 60^\circ$ and the electric field component is $E\sin \alpha$ .
Therefore, according to the above expression we have
$E\sin \alpha = \dfrac{{kp\sin 60^\circ }}{{{r^3}}}$ …..(ii)
Now, dividing equation (ii) by (i) we have
$\tan \alpha = \dfrac{{\tan 60^\circ }}{2} = \dfrac{{\sqrt 3 }}{2}$
On simplifying we have
$\alpha = {\tan ^{ - 1}}\dfrac{{\sqrt 3 }}{2}$
Now, from the figure we have
$\theta = \alpha + 60^\circ = \alpha + \dfrac{\pi }{3}$
On substituting the value of $\alpha$ we have the final answer as
$\theta = \dfrac{\pi }{3} + {\tan ^{ - 1}}\dfrac{{\sqrt 3 }}{2}$

Hence, option D is correct.

Note: The formula used for the electric field due to a dipole in this question is only valid when the distance between the charges of the dipole is very small as compared to the distance between the centre of the dipole and the point where the electric field is to be calculated.