Question

The effective resistance in series combination of two equal resistance is S. When they are joined in parallel the total resistance is $\rho$. If $S = n\rho$ then the minimum possible value of n is
(A) 4
(B) 1
(C) 2
(D) 3

Answer 1

When resistance are connected in series combination then equivalent resistance will be given as
${R_{eqn}} = {R_1} + {R_2} + {R_3} + .....$
When resistance are connected in parallel combination then equivalent resistance will be given as
$\dfrac{1}{{{R_{eqn}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + .....$

Complete step by step answer:
Given that 2 equal resistance (Let R) when connected in series then effective resistance is S i.e.,
$S = R + R = 2R$ …..(1)

When connected in parallel then effective resistance is $\rho$ i.e.,
$\dfrac{1}{\rho } = \dfrac{1}{R} + \dfrac{1}{R}$
$\dfrac{1}{\rho } = \dfrac{2}{R}$
$\rho = \dfrac{2}{R}$ …..(2)

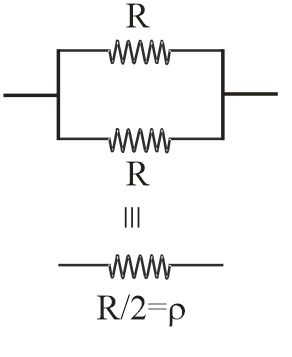
Also given that
$S = n\rho$
So, from equation 1 & 2
$2R = n\left( {\dfrac{R}{2}} \right)$
$n = \dfrac{{4R}}{R}$
$n = 4$

So, the correct answer is “Option A”.

Note:
In many problems of resistance, they can ask for current and voltage.
In series combination, the value of current in each resistance is the same.
In parallel combination, the potential difference i.e., voltage across each resistance is the same.