Question
Question: The effective resistance between A and B is (A)\(\dfrac{{7R}}{{12}}\) (B)\(\dfrac{{5R}}{7}\)...
The effective resistance between A and B is
(A)127R
(B)75R
(C)125R
(D) None of these.
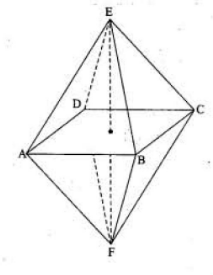
Solution
Hint: If we are provided with the huge circuit in order to simplify the circuit the effective resistance is used. Effective resistance is the measure of total resistance taken between two points.
Formula used: To solve this type of problems we use the following formula.
Requ1=R11+R21 ; This is the formula to find the equivalent resistance in parallel combination.
Requ=R1+R2 ; The formula to find equivalent resistance in the series combination.
Complete step by step answer:
First and foremost we have to find the equivalent resistance between the two ends A and B. Let R is the resistance that is connected across the edges of the given figure.
Now let us consider that potential is connected across point A and B. that implies, point E and F will be at the same potential. Therefore, using the formulas Requ1=R11+R21and Requ=R1+R2we will find the resistance across AB, as follows.
Let for our convenience we remove the resistance across AB (for some time). Then the figure looks like the following.
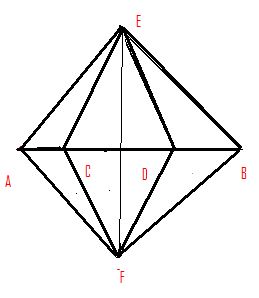
E and F will be at the same potential. So, let us draw a line joining E and F, such that it divides the resistance of DC in equal halves. That means all the points on which lie on this line joining are at the same potential.
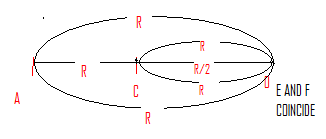
Due to symmetry, let us solve the left half for simplicity and then multiply by 2 to get the total equivalent resistance.
Rleft−half1=R1+R1+R+4R1
On solving the above expression we get the following.
Rleft−half1=5R14⇒Rleft−half=145R
So, let us write the total equivalent resistance (left half + right half) which is the following.
Requ=2×145R=1410R (Due to symmetry)
Now, the left figure is below, in which let us add the resistance R which we removed earlier for simplicity.
So from the figure, let us write the equivalent resistance across AB.
RAB1=10R14+R1
Let us simplify it.
RAB1=10R24⇒RAB=2410R=125R
Therefore, equivalent resistance across AB is 125R.
Hence, option (C) 125R is the correct option.
Note:
To calculate equivalent resistance we have two methods for two different types of circuits, series circuit and parallel circuit.
In series circuit all resistances are connected end to end. So equivalent resistance is obtained by the following formula.
Requ=R1+R2
In a parallel circuit, all resistances are connected across each other forming exactly two common points. So, equivalent resistance is obtained by the following formula.
Requ1=R11+R21
