Question

The effective resistance between A and B is:

(A) $10\Omega$
(B) $20\Omega$
(C) $30\Omega$
(D) $20.2\Omega$

Answer 1

In order to solve this question, we will be using the laws of addition of resistances in series as well as in parallel. We will be solving the question step by step and find the equivalent resistance between A and B.
The formulae to add the resistances in series and parallel are given respectively as
$R={{R}_{1}}+{{R}_{2}}$
And $\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$ .

Complete step by step answer:
Now using the law of addition of resistances, we will be dividing the circuits and then solving.

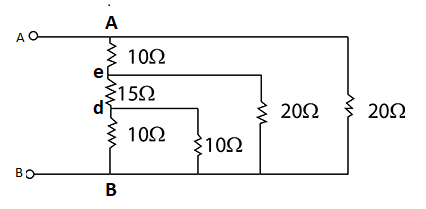
Therefore, first of all we will name the points d and e in the circuit as shown in the figure.
Now, our first step will be calculating the equivalent resistance across B-d. The two resistances connecting the points B and d are in parallel with each other and so, using the law for addition of resistances who are in parallel, we get
$\begin{aligned} & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \\\ & \Rightarrow \dfrac{1}{{{R}_{eBd}}}=\dfrac{1}{10}+\dfrac{1}{10} \\\ & \Rightarrow \dfrac{1}{{{R}_{eBd}}}=\dfrac{1}{5} \\\ & \Rightarrow {{R}_{eBd}}=5\Omega \\\ \end{aligned}$
Now, our next step will be to calculate the equivalent resistance across B-e. The two resistances that will be in series with each other, i.e., ${{R}_{ed}}$ is in series with ${{R}_{eBd}}$ . And these two resistances are in parallel with the other resistance in B-e. Therefore, calculating the equivalent resistance of B-e, we get
$\begin{aligned} & {{R}_{Be}}={{R}_{eBd}}+{{R}_{de}} \\\ & \Rightarrow {{R}_{eB}}=5+15 \\\ & \Rightarrow {{R}_{eB}}=20\Omega \\\ \end{aligned}$
And
$\begin{aligned} & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \\\ & \Rightarrow \dfrac{1}{{{R}_{eBe}}}=\dfrac{1}{20}+\dfrac{1}{20} \\\ & \Rightarrow \dfrac{1}{{{R}_{eBe}}}=\dfrac{2}{20} \\\ & \Rightarrow {{R}_{eBe}}=10\Omega \\\ \end{aligned}$
Now, the third and our final step will be to calculate the equivalent resistance across B-A. The two resistances that will be in series with each other, i.e., ${{R}_{Ae}}$ are in series with ${{R}_{eBe}}$ . And these two resistances are in parallel with the other resistance in B-A. Therefore, calculating the equivalent resistance of B-A, we get
$\begin{aligned} & {{R}_{BA}}={{R}_{eBe}}+{{R}_{Ae}} \\\ & \Rightarrow {{R}_{BA}}=10+10 \\\ & \Rightarrow {{R}_{BA}}=20\Omega \\\ \end{aligned}$
And
$\begin{aligned} & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \\\ & \Rightarrow \dfrac{1}{{{R}_{eBA}}}=\dfrac{1}{20}+\dfrac{1}{20} \\\ & \Rightarrow \dfrac{1}{{{R}_{eBA}}}=\dfrac{2}{20} \\\ & \Rightarrow {{R}_{eBA}}=10\Omega \\\ & \\\ \end{aligned}$
Therefore, the answer to our question will be option (A).

Note:
Keep in mind to use the equivalent resistance calculated for each part in the following next calculation and also to look and evaluate the figure according to the calculations. The subscript $e$ in the calculation is for the equivalent resistance.