Question
Question: The effective resistance between A and B in given circuit is: (A) \( 20\Omega \) (B) \( 7\Omega...
The effective resistance between A and B in given circuit is:
(A) 20Ω
(B) 7Ω
(C) 3Ω
(D) 6Ω
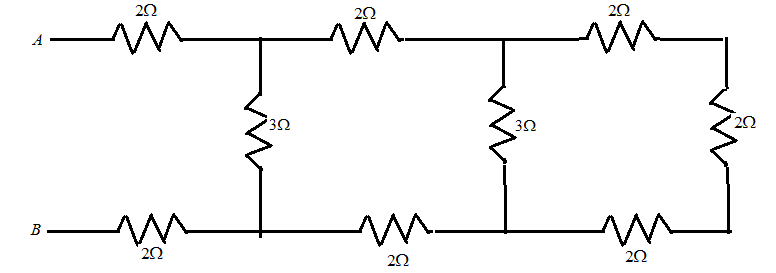
Solution
Hint : We know how to solve the series and parallel combination of resistors in any circuit. But here we have the resistors in combination of parallel and series as well. To solve this type of problem we have to break them into series parts and solve them repeatedly.
Complete Step By Step Answer:
Let us consider the figure given below and solve a rounded part first
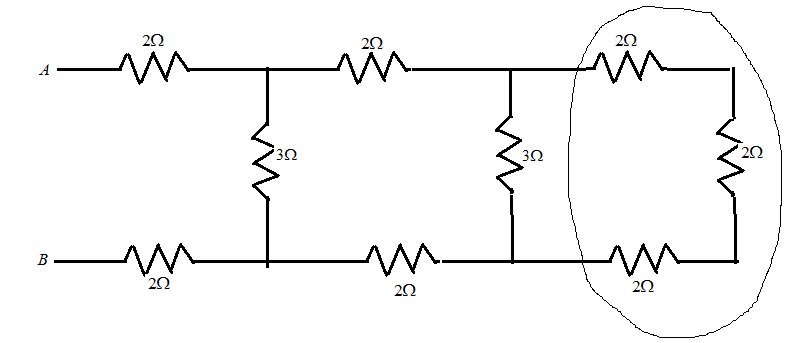
Therefore, resultant resistance of resistors in series combination is
Req=R1+R2+R3
∴Req=6Ω
Now, In the diagram we simplified the rounded part and it is connected in parallel with the resistor of 3Ω .
Therefore let us now simplify the parallel combination of 6Ω and 3Ω .
Req=R1+R2R1×R2 =6+36×3 =2Ω
Now this 2Ω will be in series with other two resistors of 2Ω and 2Ω
Therefore, the equivalent resistance is given by
Req=R1+R2+R3
∴Req=6Ω
Again this 6Ω is in parallel combination with the 3Ω after solving this we get,
Req=R1+R2R1×R2 =6+36×3 =2Ω
Now, here we simplified the circuit and now we have the small part remaining to solve as given below:
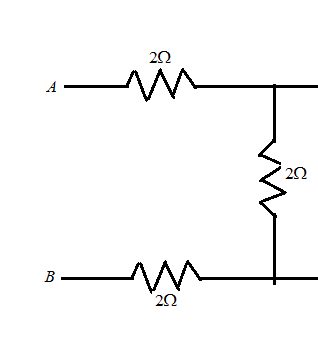
Between A and B we have the resistors of 2Ω , 2Ω , 2Ω are in series combination, to solve this we have to apply the formula of series combination and then we get,
Req=R1+R2+R3
∴Req=6Ω
Therefore, the total equivalent resistance between A and B is 6Ω .
Thus, the correct option is D.
Note :
The resistance in these types of circuit is calculated by resolving them part by part. You must have an idea how to classify the parallel combination and series combination of resistors. Series combination is when the resistors are connected adjacently between two points and parallel is when the resistors are connected parallel between two points.
