Question

The effective focal length of the lens combination shown in the figure is $60cm$ . The radii of curvature of the curved surfaces of the Plano-convex lenses are $12cm$ each and the refractive index of the material of the lens is $1.5$ . The refractive index of the liquid is:

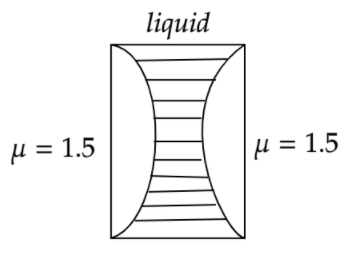
A) $1.33$
B) $1.42$
C) $1.53$
D) $1.60$

Answer 1

In case of using a single lens, there is only one optical element. In contrast to this, a compound lens is an array or combination of simple lenses having a common axis. Usually, the lenses are placed in contact with each other but sometimes we put a material between the lenses such as done in this question. In the case of lens combination, the powers of the lenses are added.

Formula Used:
$\dfrac{1}{f}=\dfrac{2}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$ , $\dfrac{1}{f}=\left( {{\mu }_{2}}-{{\mu }_{1}} \right)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$

Complete step by step solution:
We know that power of a lens is the reciprocal of its focal length and the powers in a lens combination are added. Hence we can say that the effective power of the combination will be equal to the sum of the powers of the two Plano-convex lenses and the power of the concave lens which the liquid is forming. Mathematically, $P=2{{P}_{1}}+{{P}_{2}}$ where ${{P}_{1}}$ is the power of the Plano-convex lens, ${{P}_{2}}$ is the power of the lens formed by the liquid and $P$ is the effective power of the combination
Substituting power by the reciprocal of focal lengths, we get
$\dfrac{1}{f}=\dfrac{2}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$ where ${{f}_{1}}$ and ${{f}_{2}}$ are the focal lengths of the Plano-convex lenses $--equation(1)$
It is to be noted that for the plane surface of the Plano-convex lenses, the radius of curvature of the surface will be infinite, that is ${{R}_{plane}}=\infty$
Hence, the reciprocal of the radius of the plane surface will be zero, since $1/\infty =0$ , and can be neglected
The expression for the focal lengths of the lenses can be written as,
$\dfrac{1}{{{f}_{1}}}=\left( \mu -1 \right)\dfrac{1}{R}$ and $\dfrac{1}{{{f}_{2}}}=\left( {{\mu }_{L}}-1 \right)\dfrac{1}{R}$ where $\mu$ stands for the refractive index of the lens and ${{\mu }_{L}}$ stands for the refractive index of the liquid
The effective focal length of the combination is given to be $60cm$ , that is, $f=60cm$
The radius of curvature of the curved surfaces $(R)=12cm$
The values of the focal lengths will be as given below

& \dfrac{1}{{{f}_{1}}}=\left( 1.5-1 \right)\dfrac{1}{12} \\\ & \Rightarrow \dfrac{1}{{{f}_{1}}}=\dfrac{1}{24} \\\ \end{aligned}$$ Similarly, for the lens formed by the liquid, we have $$\begin{aligned} & \dfrac{1}{{{f}_{2}}}=\left( {{\mu }_{L}}-1 \right)\dfrac{-2}{12} \\\ & \Rightarrow \dfrac{1}{{{f}_{2}}}=\dfrac{-\left( {{\mu }_{L}}-1 \right)}{6} \\\ \end{aligned}$$ Substituting these values in $$equation(1)$$ , we get $$\begin{aligned} & \dfrac{1}{f}=\dfrac{2}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}} \\\ & \Rightarrow -\dfrac{1}{60}=\dfrac{2}{24}-\dfrac{\left( {{\mu }_{L}}-1 \right)}{6} \\\ & \Rightarrow -\dfrac{1}{60}=\dfrac{1-2\left( {{\mu }_{L}}-1 \right)}{12} \\\ & \Rightarrow 1-2\left( {{\mu }_{L}}-1 \right)=-\dfrac{1}{5} \\\ & \Rightarrow 10\left( {{\mu }_{L}}-1 \right)-5=1 \\\ & \Rightarrow \left( {{\mu }_{L}}-1 \right)=0.6 \\\ & \Rightarrow {{\mu }_{L}}=1.6 \\\ \end{aligned}$$ **Hence (D) is the correct option.** **Note:** The most common error which students make in such problems is in the substitution of the values of focal length and the radius of curvature. The sign convention is extremely important in numerical optics since one misplaced minus sign can waste the entire effort put into the question. The distance measured along the direction of motion of light ray is taken to be positive and those opposite are taken negatively.