Question

The effective capacitance between A and B will be

A. 0.5F
B. 1.5F
C. 2F
D. 2.5F

Answer 1

As a first step, you could recall the expression for effective capacitance of parallel and series combination of capacitors. Then you could approach the combination part by part considering series and parallel combinations. Now apply the above expression for each part and thus find the effective capacitance of the combination.

Formulae used:
Effective capacitance,
For parallel,
${{C}_{eff}}={{C}_{1}}+{{C}_{2}}$
For series,
$\dfrac{1}{{{C}_{eff}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$

Complete Step by step solution:
In the question, we are asked to find the effective resistance across terminals A and B.
Before answering the question, let us recall the effective capacitance of parallel and series combinations.

When two capacitors are connected in series, then the effective capacitance is given by,
$\dfrac{1}{{{C}_{eff}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$

When two capacitors are connected in parallel, then the effective capacitance is given by,
${{C}_{eff}}={{C}_{1}}+{{C}_{2}}$

Now, let us reduce the given combination step by step.

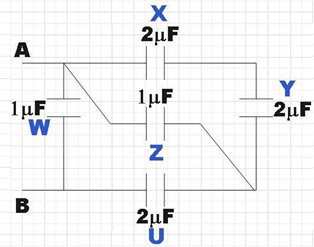
We see that in the given combination, capacitors X and Y are connected in series. So the effective capacitance will be,
${{C}_{XY}}=\dfrac{{{C}_{X}}{{C}_{Y}}}{{{C}_{X}}+{{C}_{Y}}}$
$\Rightarrow {{C}_{XY}}=\dfrac{2\times 2}{2+2}$
$\therefore {{C}_{XY}}=\dfrac{4}{4}=1\mu F$

Now, we see that ${{C}_{XY}}$ is connected parallel with capacitor Z, their effective capacitance would be,
${{C}_{XYZ}}={{C}_{XY}}+{{C}_{Z}}$
$\Rightarrow {{C}_{XYZ}}=1+1$
$\therefore {{C}_{XYZ}}=2\mu F$

Now the circuit would look as shown below,

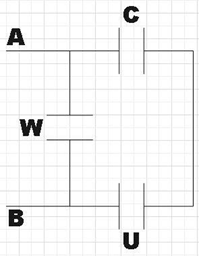
The capacitance C here is the capacitor${{C}_{XYZ}}$. We see that capacitor C is connected in series with capacitor U. Their effective capacitance would be,
${{C}_{UC}}=\dfrac{UC}{U+C}$
$\Rightarrow {{C}_{UC}}=\dfrac{2\times 2}{2+2}$
$\therefore {{C}_{UC}}=1\mu F$

Now we see that ${{C}_{UC}}$ is connected in parallel with capacitor W.
${{C}_{eff}}={{C}_{UC}}+{{C}_{W}}$
$\Rightarrow {{C}_{eff}}=1+1$
$\therefore {{C}_{eff}}=2\mu F$

Therefore, we found that the effective capacitance of the given combination to be $2\mu F$.

Hence, option C is found to be the correct answer.

Note:
Capacitance can be defined as the ratio of electric charge that is stored in a conductor to the potential difference across it. It could be otherwise defined as the ability of the body to hold an electric charge. The SI unit of capacitance is known to be Farad (F). The capacitance of the capacitor is dependent on its geometry.