Question

The effective capacitance between A and B will be

A. 6C
B. 4C
C. 2C
D. none of the above

Answer 1

We are given a circuit which consists of capacitors connected to it. In order to find the solution, let us make two portions of the circuit. We can see that the bottom portion is the Wheatstone bridge network. It is a simple circuit used for measuring an unknown resistance by connecting it in order to form a quadrilateral with three known resistances and applying a voltage between a pair of opposite corners.

Complete answer:
So, we will apply the balancing condition to calculate the equivalent capacitance of the bottom part. Then, to calculate the capacitance between A and B we will take the parallel combination.
Let us name each capacitor in order to make the solution easy,

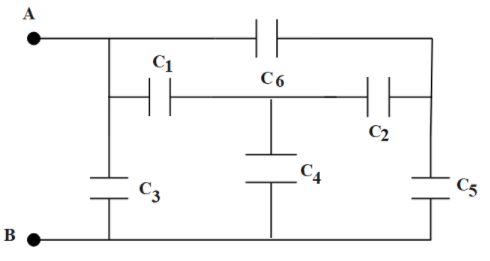
From the circuit, ${C_4}$ is connected parallelly with the rest of the combined capacitors. So, we will draw a simplified circuit

Here, $C'$is the combined capacitance of the capacitors excluding ${C_4}$.
Now, we see that the rest of the circuit is equivalent to the Wheatstone bridge network. So, when we will apply the balance condition to the Wheatstone network, then ${C_3}$ could be neglected.
Now, the resulting circuit we will get is,

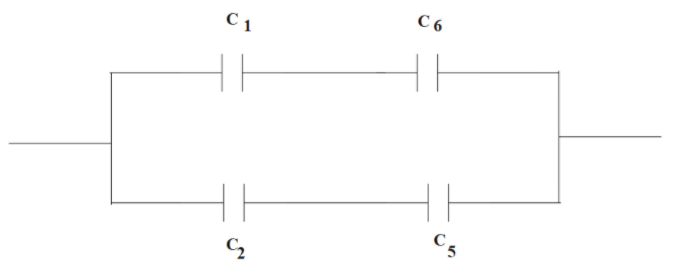
Using the series combination in the upper portion we will find the equivalent capacitance,
\eqalign{ & \dfrac{1}{{C''}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_6}}} \cr & \Rightarrow \dfrac{1}{{C''}} = \dfrac{{{C_1} + {C_6}}}{{{C_1} \times {C_6}}} \cr & \Rightarrow C'' = \dfrac{{{C_1} \times {C_6}}}{{{C_1} + {C_6}}} \cr}
Similarly, using the series combination in the bottom portion we will find the equivalent capacitance,
\eqalign{ & \dfrac{1}{{C'''}} = \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_5}}} \cr & \Rightarrow \dfrac{1}{{C'''}} = \dfrac{{{C_2} + {C_5}}}{{{C_2} \times {C_5}}} \cr & \Rightarrow C''' = \dfrac{{{C_2} \times {C_5}}}{{{C_2} + {C_5}}} \cr}
As we can see that $C''$ and $C'''$are in series so equivalent capacitance is given as,
\eqalign{ & C' = C'' + C''' \cr & \Rightarrow C' = \dfrac{{{C_1}{C_6}}}{{{C_1} + {C_6}}} + \dfrac{{{C_2}{C_5}}}{{{C_2} + {C_5}}} \cr}
Since, ${C_1} = {C_6} = {C_2} = {C_5} = C$
\eqalign{ & C' = \dfrac{{C.C}}{{C + C}} + \dfrac{{C.C}}{{C + C}} \cr & \Rightarrow C' = \dfrac{{{C^2}}}{{2C}} + \dfrac{{{C^2}}}{{2C}} \cr & \Rightarrow C' = \dfrac{C}{2} + \dfrac{C}{2} \cr & \Rightarrow C' = C \cr}
$\therefore {C_{eq}} = {C_4} + C = C + C = 2C$
Thus, the effective capacitance between A and B will be 2C.

Hence, option (C) is the correct answer.

Note:
A capacitor is defined as an electrical component which connects the circuit. It is used to store the charge and also to accumulate the charge. It is a system which consists of two conductors.