Solveeit Logo
Login

Question

Question: The edge of an aluminum cube is \[10cm\] long. One face of the cube is fixed to a vertical wall. A m...

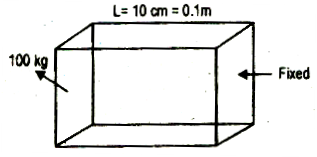
The edge of an aluminum cube is 10cm10cm long. One face of the cube is fixed to a vertical wall. A mass of 100kg100kg is then attached to the opposite facet of the cube. The shear modulus of aluminum is 25Gpa25Gpa. What is the vertical deflection of this face?

Explanation

Solution

Lateral strain is also known as transverse strain. The ratio of the change in diameter of a circular bar of a material to its diameter due to deformation in the longitudinal direction is called lateral strain. We know that the shear modulus is defined as the ratio of Tangential stress to the shearing strain. And similarly, we know that the shearing strain is defined as the ratio of Lateral strain to the side of the cube. By applying these formulae we can find out the vertical deflection of this face.

Formula used:
Shearing Strain == Tangential Stress / Shear modulus
⇒FAη\Rightarrow \dfrac{F}{{A\eta }}, Where F=F = Tangential Stress, η=\eta = Shear modulus, A=A = Area of each face
Lateral Strain == Shearing Strain×\times Side of the cube

Complete step-by-step solution:
Here, side of the cube, L=10cm=0.1mL = 10cm = 0.1m
Area of each face A=(0.1)2=0.01m2A = {\left( {0.1} \right)^2} = 0.01{m^2}
The tangential force acting on the face, F=100kg=100×9.8=980NF = 100kg = 100 \times 9.8 = 980N

Shear modulus, \eta $$$$ = Tangential stress / Shearing strain
Shearing strain = Tangential stress / Shear modulus
⇒FAη=9800.01×25×109\Rightarrow \dfrac{F}{{A\eta }} = \dfrac{{980}}{{0.01 \times 25 \times {{10}^9}}}
=3.92×10−6= 3.92 \times {10^{ - 6}}
Now, The lateral strain/side of the cube = shearing strain
Lateral strain = Shearing strain ×\timesside of the cube
=3.92×10−6×0.1= 3.92 \times {10^{ - 6}} \times 0.1
=3.92×10−7m= 3.92 \times {10^{ - 7}}m
Hence, the vertical deflection of this face is 3.92×10−7m3.92 \times {10^{ - 7}}m.

Note: The force acting on a moving body in the direction of the tangent to the curved path of the body is called the Tangential force.
A material can resist transverse deformations and is a valid index of elastic behavior only for small deformations, after which the material can return to its original configuration is defined as the shear modulus.
The vertical distance between a point from the unreformed axis of a structure and the same point which lies on the deformed axis is called the vertical deflection.