Question

The eccentricity of the ellipse ${x^2} + 4{y^2} + 2x + 16y + 13 = 0$ is?
A. $\dfrac{{\sqrt 3 }}{2}$
B. $\dfrac{1}{2}$
C. $\dfrac{1}{{\sqrt 3 }}$
D. $\dfrac{1}{{\sqrt 2 }}$

Answer 1

Hint : To find the eccentricity of the ellipse, first convert the given equation into the form $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$. If the value of a is greater than b, then the eccentricity e is calculated using $e = \dfrac{{\sqrt {{a^2} - {b^2}} }}{a}$ and if the value of b is greater than a, then the eccentricity e is calculated using $e = \dfrac{{\sqrt {{b^2} - {a^2}} }}{b}$

Complete step-by-step answer :

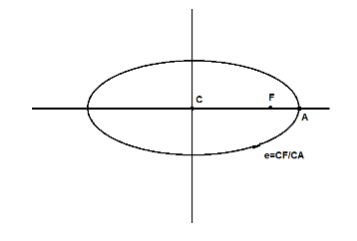
The eccentricity of an ellipse is the ratio of distance from the centre to one of the foci and to one of the vertices of the ellipse.
We are given an equation of ellipse ${x^2} + 4{y^2} + 2x + 16y + 13 = 0$
We have to convert the above equation into $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ form
${x^2} + 4{y^2} + 2x + 16y + 13 = 0$
Here as we can see, there are two variables x and y in the above equation.
Arrange the terms with similar variables together.
$\to {x^2} + 2x + 4{y^2} + 16y + 13 = 0$
The expansion of ${\left( {a - b} \right)^2}$ is ${a^2} - 2ab + {b^2}$
So to convert the above equation into general form we have to convert it into two ${\left( {a - b} \right)^2}$ forms with x and y variables.
${x^2} + 2x + 4{y^2} + 16y + 13 = 0 \\\ \to {x^2} + \left( {2 \times x \times 1} \right) + {\left( {2y} \right)^2} + \left( {2 \times 2y \times 4} \right) + 13 = 0 \\\$
We need an extra 4 to convert it into general form. So add 4 on the left hand side and right hand side.
${x^2} + \left( {2 \times x \times 1} \right) + {\left( {2y} \right)^2} + \left( {2 \times 2y \times 4} \right) + 13 + 4 = 0 + 4 \\\ \to {x^2} + \left( {2 \times x \times 1} \right) + {\left( {2y} \right)^2} + \left( {2 \times 2y \times 4} \right) + 17 = 4 \\\ \to {x^2} + \left( {2 \times x \times 1} \right) + 1 + {\left( {2y} \right)^2} + \left( {2 \times 2y \times 4} \right) + 16 = 4 \\\ \to {x^2} - \left( {2 \times x \times - 1} \right) + {\left( { - 1} \right)^2} + {\left( {2y} \right)^2} - \left( {2 \times 2y \times - 4} \right) + {\left( { - 4} \right)^2} = 4 \\\$
The above equation has two ${a^2} - 2ab + {b^2}$ forms, replace them with their ${\left( {a - b} \right)^2}$ forms
${\left( {x - \left( { - 1} \right)} \right)^2} + {\left( {2y - \left( { - 4} \right)} \right)^2} = 4 \\\ {\left( {x + 1} \right)^2} + {\left( {2y + 4} \right)^2} = 4 \\\$
Divide both sides by 4
$\dfrac{{{{\left( {x + 1} \right)}^2} + {{\left( {2y + 4} \right)}^2}}}{4} = \dfrac{4}{4} \\\ \to \dfrac{{{{\left( {x + 1} \right)}^2}}}{4} + \dfrac{{{{\left( {2y + 4} \right)}^2}}}{4} = 1 \\\$
Take out 4 from the second term
$\dfrac{{{{\left( {x + 1} \right)}^2}}}{4} + \dfrac{{4{{\left( {y + 2} \right)}^2}}}{4} = 1 \\\ \to \dfrac{{{{\left( {x + 1} \right)}^2}}}{4} + \dfrac{{{{\left( {y + 2} \right)}^2}}}{1} = 1 \\\ \to \dfrac{{{{\left( {x + 1} \right)}^2}}}{{{2^2}}} + \dfrac{{{{\left( {y + 2} \right)}^2}}}{{{1^2}}} = 1 \\\$
On comparing the above equation with $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$, we get the value of a=2 and b=1.
The value of a is greater than b, so the eccentricity e is $e = \dfrac{{\sqrt {{a^2} - {b^2}} }}{a}$
$e = \dfrac{{\sqrt {{a^2} - {b^2}} }}{a} \\\ a = 2,b = 1 \\\ \to e = \dfrac{{\sqrt {{2^2} - {1^2}} }}{2} \\\ \to e = \dfrac{{\sqrt {4 - 1} }}{2} \\\ \therefore e = \dfrac{{\sqrt 3 }}{2} \\\$
The correct option is Option A, $\dfrac{{\sqrt 3 }}{2}$
So, the correct answer is “Option A”.

Note : Concentricity is almost similar to eccentricity but has only one difference which is concentricity has only magnitude but no direction whereas eccentricity has both magnitude and direction. The value of concentricity is twice the value of eccentricity. So do not confuse between these two.