Question
Question: The eccentricity of an ellipse, with its Centre at the origin, is \(\dfrac{1}{2}\). If one of the di...
The eccentricity of an ellipse, with its Centre at the origin, is 21. If one of the directrices is x=4 , then the equation of the ellipse is:
Solution
From the question given we have been asked to find the equation of the ellipse having Centre at the origin, with eccentricity 21, and one of the directrices is x=4. as we know that the general equation of ellipse having centre as origin isa2x2+b2y2=1, here a>ba>b because the directrix is parallel to y axis. And also, we know that the formula b2=a2(1−e2), and also, we know that the directrix x-coordinate will be equal to ea. From all this we will get the equation of ellipse.
Complete step by step solution:
From the question given that the eccentricity of the ellipse having centre as origin is,
⇒e=21
And also given that the one of the directrices is
⇒x=4
As we know that the x-coordinate of directrix is equal to
⇒ea
By this we will get the value of “a” as we know the value of e,
⇒ea=4
⇒a=4e
⇒a=4×21
⇒a=2
To find the value of “b” as we know that the formula,
⇒b2=a2(1−e2)
Now, by substituting the values in their respective position we will get,
⇒b2=(2)2(1−(21)2)
By simplifying further, we will get,
⇒b2=4(1−41)
⇒b2=4(43)
⇒b2=3
Therefore, we know that the general equation of the ellipse having centre as origin is,
⇒a2x2+b2y2=1
Now by substituting the values of “a” and “b”, we will get the required ellipse equation,
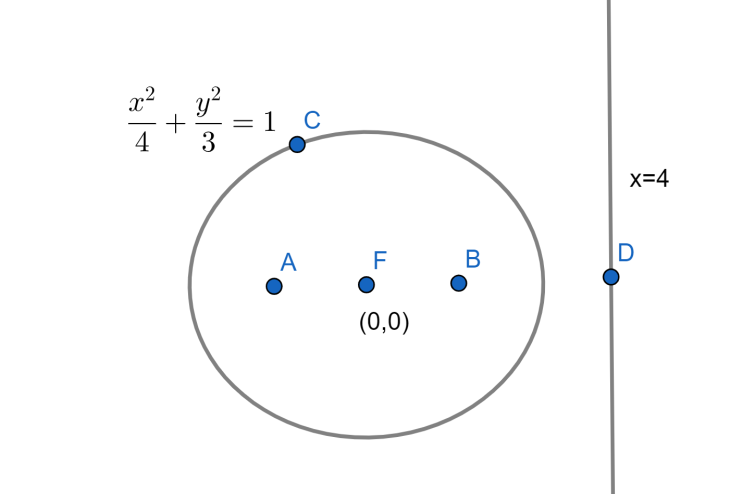
⇒4x2+3y2=1
By further simplifying we will get,
⇒3x2+4y2=12
Therefore, this is the required ellipse equation.
The figure would be as follows.
Note: students should recall the all the formulas of ellipse before doing this problem, students should know also note that the general equation of ellipse having origin as (h,k) is a2(x−h)2+b2(y−k)2=1.
