Question

The earth is considered as a short magnet with its centre coinciding with the geometric centre of the earth. The angle of dip $\phi$ related to the magnetic latitude $\lambda$ as:
A) $\tan \phi =\dfrac{1}{2\tan \alpha }$
B) $\tan \lambda =\tan \phi$
C) $\tan \lambda =2\tan \phi$
D) $\tan \phi =2\tan \lambda$

Answer 1

Magnetic dip or angle of dip is the angle made by the Earth's magnetic field lines with the horizontal. This angle is different at different points on the surface of the Earth. A positive value for the angle of dip implies that the magnetic field of the Earth is pointing inwards at the point of measurement, and a negative value indicates that it is pointing upward.

Formula Used:
${{B}_{E}}=\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{2M}{{{R}^{3}}}$ , ${{B}_{A}}=\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{M}{{{R}^{3}}}$ , $\tan \phi =\dfrac{\text{vertical field}}{\text{horizontal field}}=-\dfrac{\text{equatorial component}}{\text{axial component}}$

Complete step by step solution:

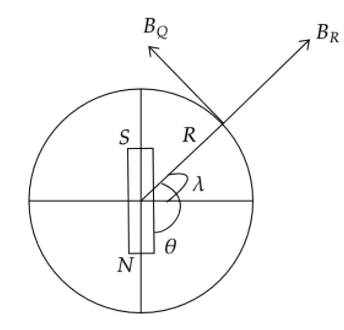
In the diagram above,
The source of the earth’s magnetic field can be seen as a bar magnet placed at the core with its centre coinciding with the geometric centre of the earth.
The equatorial field of the bar magnet can be given as ${{B}_{E}}=\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{2M}{{{R}^{3}}}$ where $M$ is the magnetic moment of the bar magnet and $R$ is the radius of the earth.
The axial field of the earth can be given as ${{B}_{A}}=\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{M}{{{R}^{3}}}$.
The equatorial and the axial components of the field at a point P on the earth’s surface can be given as $\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{2M\cos \theta }{{{R}^{3}}}$ and $\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{M\sin \theta }{{{R}^{3}}}$ respectively.

Hence at P, the resultant magnetic field can be given as ${{B}_{P}}=\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{2M\cos \theta }{{{R}^{3}}}\overrightarrow{i}+\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{M\sin \theta }{{{R}^{3}}}\overrightarrow{j}$ where $\theta$ is the angle the radial position of the point P makes with the vertical axis of the earth.
As discussed above, $\tan \phi =-\dfrac{\text{equatorial component}}{\text{axial component}}$ where $\phi$ is the angle of dip
Substituting the values, we get

& \tan \phi =-\dfrac{\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{2M\cos \theta }{{{R}^{3}}}}{\dfrac{{{\mu }_{0}}}{4\pi }\times \dfrac{M\sin \theta }{{{R}^{3}}}} \\\ & \Rightarrow \tan \phi =-\dfrac{2\cos \theta }{\sin \theta } \\\ & \Rightarrow \tan \phi =-2\cot \theta \\\ \end{aligned}$$ From the given diagram, we have $$\theta =90{}^\circ +\lambda $$ where $$\lambda $$ is the angle the radial position of the point P makes with the horizontal axis of the earth or the equator. Simplifying the expression obtained above, we get $$\begin{aligned} & \tan \phi =-2\cot (90{}^\circ +\lambda ) \\\ & \Rightarrow \tan \phi =2\tan \lambda \left[ \because \cot (90{}^\circ +\lambda )=-\tan \lambda \right] \\\ \end{aligned}$$ **Hence, the option (D) is the correct answer.** **Note:** Earth’s magnetic field is caused by a dynamo effect. The effect can be considered similar to a dynamo light on a bicycle. Magnets in the dynamo spin when the bicycle is in motion, creating an electric current. The rotation of Earth on its axis causes these electric currents to give rise to a magnetic field.