Question

The driver of a train travelling at $115km/hr$ sees on the same track $100m$ in front of him, a slow train travelling in the same direction at $25km/hr$. What is the least retardation to be applied to the faster train to avoid collision?

Answer 1

In this case, to avoid collision the faster train should come to rest just before reaching the slower train. So given the conditions that there is a separation between them and the speeds of the trains we need to apply the kinematics equations to solve the problem. Let’s start solving the question.
Formula used:
$s=ut+\dfrac{1}{2}a{{t}^{2}},v=u-at$

Complete answer:

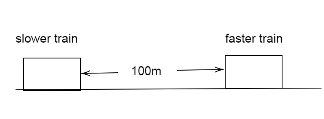
Let the least retardation applied on the faster train be $a$. Let the faster train come to rest after $ts$ pulling the break. In this time the slower train moves a distance, as the separation between them is $100m$ the faster train moves extra $100m$ in that time.

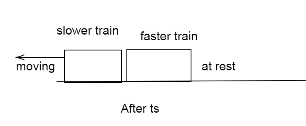
Now the speed of the faster train is
$\dfrac{115km}{hr}=\dfrac{115\times 1000}{3600}m{{s}^{-1}}=\dfrac{575}{18}m{{s}^{-1}}$
The speed of the slower train is
$25km/hr=\dfrac{25\times 1000}{3600}m{{s}^{-1}}=\dfrac{125}{18}m{{s}^{-1}}$
Thus we can write
$\dfrac{125}{18}\times t+100=\dfrac{575}{18}\times t-\dfrac{1}{2}a{{t}^{2}}$ ………..$(1)$
And
$0=\dfrac{575}{18}-at$ ………..$(2)$
Now putting the value of $at$ from $(2)$ into $(1)$ we get
$\begin{aligned} & \dfrac{125}{18}\times t+100=\dfrac{575}{18}\times t-\dfrac{1}{2}\times \dfrac{575}{18}\times t \\\ & \Rightarrow 100=(\dfrac{575}{36}-\dfrac{125}{18})t \\\ & \Rightarrow t=\dfrac{144}{13}s \\\ \end{aligned}$
Now putting the value of $t$ in $(2)$ we get
$\begin{aligned} & 0=\dfrac{575}{18}-\dfrac{144}{13}a \\\ & \Rightarrow a=2.88m{{s}^{-2}} \\\ \end{aligned}$
Thus minimum retardation that is needed to be applied to the faster train is $2.88m{{s}^{-2}}$.

Note:
Here we first need to convert all the velocities in SI. It is to be remembered that only the faster train will come to rest after the time $t$. The slower train will go faster. We must add an extra 100 m distance travelled by the faster train at time $t$ to get the correct equation.