Question

The driver of a car travelling at a speed of 20 m/s, wishes to overtake a truck that is moving with a constant speed of 20 m s$^{-1}$ in the same lane. The cars maximum acceleration is 0.5 m s$^{-2}$. Initially the vehicles are separated by 40 m, and the car returns back into its lane after it is 40 m ahead of the truck. The car is 3 m long and the truck 17 m long. Find the minimum time required for the car to pass the truck and return back to its lane?

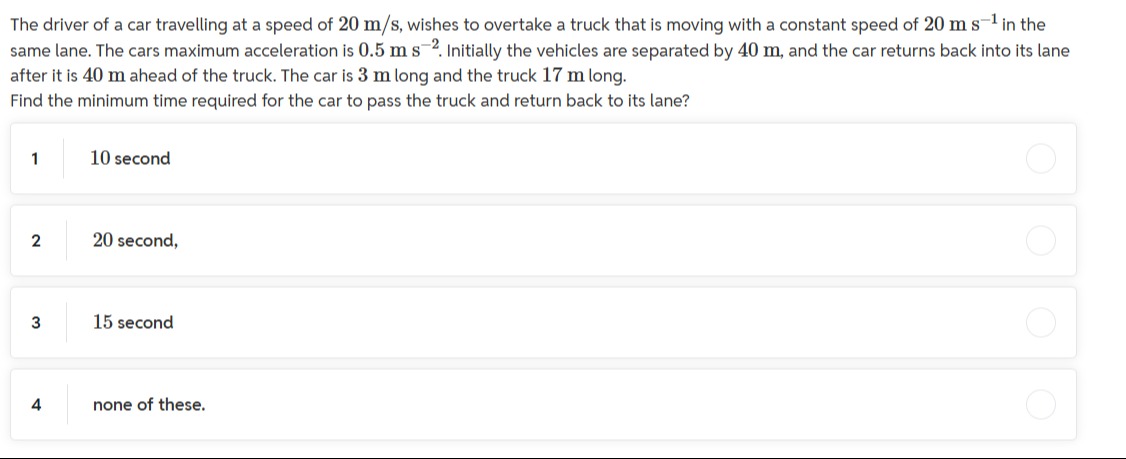
• A. 10 second
• B. 20 second
• C. 15 second
• D. none of these.

Answer 1

Answer: (B)

20 second

Answer 2

Let $v_c$ be the initial velocity of the car and $v_t$ be the velocity of the truck. $v_c = 20$ m/s, $v_t = 20$ m/s. Maximum acceleration of the car, $a_c = 0.5$ m/s$^2$. Length of car, $L_c = 3$ m. Length of truck, $L_t = 17$ m.

Let $t=0$ be the instant the car starts its overtaking maneuver. We define positions relative to the ground. Let the rear of the truck be at $x=0$ at $t=0$.

• Position of truck's rear at $t=0$: $x_{tr}(0) = 0$.
• Position of truck's front at $t=0$: $x_{tf}(0) = L_t = 17$ m.
• The car is initially separated by 40 m from the truck. This means the front of the car is 40 m behind the rear of the truck. Position of car's front at $t=0$: $x_{cf}(0) = -40$ m.
• Position of car's rear at $t=0$: $x_{cr}(0) = x_{cf}(0) - L_c = -40 - 3 = -43$ m.

The truck moves with constant velocity: $x_{tf}(t) = x_{tf}(0) + v_t t = 17 + 20t$.

The car starts with $v_c(0) = 20$ m/s and accelerates at $a_c = 0.5$ m/s$^2$. To find the minimum time, the car must use its maximum acceleration throughout the maneuver. The position of the car's rear at time $t$ is given by: $x_{cr}(t) = x_{cr}(0) + v_c(0)t + \frac{1}{2}a_c t^2$ $x_{cr}(t) = -43 + 20t + \frac{1}{2}(0.5)t^2$ $x_{cr}(t) = -43 + 20t + 0.25t^2$.

The overtaking is complete when the car is 40 m ahead of the truck. This means the rear of the car is 40 m ahead of the front of the truck. The condition is: $x_{cr}(t) - x_{tf}(t) = 40$.

Substitute the expressions for $x_{cr}(t)$ and $x_{tf}(t)$: $(-43 + 20t + 0.25t^2) - (17 + 20t) = 40$. $-43 + 20t + 0.25t^2 - 17 - 20t = 40$. Combine terms: $-60 + 0.25t^2 = 40$. $0.25t^2 = 40 + 60$. $0.25t^2 = 100$. $t^2 = \frac{100}{0.25} = 100 \times 4 = 400$. $t = \sqrt{400} = 20$ seconds.

This is the minimum time required for the car to overtake the truck and return to its lane according to the specified conditions.