Question

The door of an almirah is 6ft height, 1.5 ft wide and weighs 8kg. The door is supported by the 2 hinges situated at the distance of 1ft from the ends. If the magnitudes of the forces exerted by the hinges on the door are equal, find this magnitude.
(A) 36N
(B) 50N
(C) 40N
(D) 43N

Answer 1

Hint
Dimensions of the door are given. We will apply the concept of normal, resultant force along horizontal and vertical. We will use $\tau = r \times F\sin \theta$ to calculate torque acting on the door then magnitude of resultant force is calculated using the vector law of addition.

Complete step by step answer

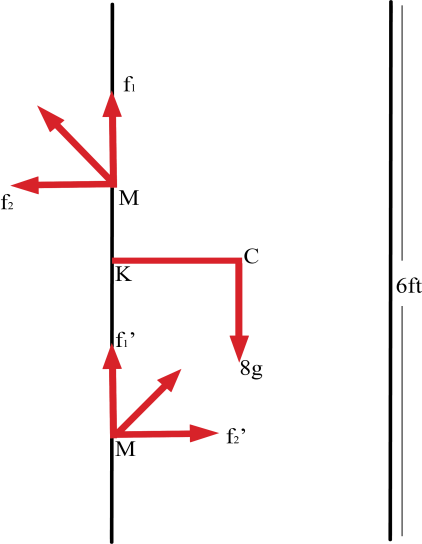
Let us assume the position of hinges are M and N respectively. Centre of mass of door be C which lies at position (3,0.79).
Forces exerted on the door are F and F’.
Let us assume the horizontal and vertical component of forces acting on door be and .
Door rotates with the help of a couple, it is provided by a horizontal component of forces.
So , ${f_2} = {f_2}’$ …(1)
and vertical component will be equal to weight of door
Then, ${f_1} + {f_1}' = 8g$ …(2)
Magnitude of the forces exerted by hinges on the door are equal , $F = F'$ (given) …(3)
=> ${f_1} = {f_1}'$ …(4)
Using (4) in (1), we get
${f_1} = {f_1}' = \dfrac{{8g}}{2} = 4g = 40N$
$\left( {g = \dfrac{{10m}}{{{{\sec }^2}}}} \right)$
Torque acting on the axis passing through point N and perpendicular to MN is zero. $\tau = - MN.{f_2} + 8KC$
${f_2} = 15N$
From equation (4)
$F = F' = \sqrt {{f_1}^2 + {f_2}^2} = \sqrt {{{15}^2} + {{40}^2}} = 43N$
Thus, the correct option is (D).

Note
It is important to change dimensions of foot into meter as force in options are given in Newton. If we do not draw a free body diagram then it might affect understanding of concept and values might alter the result. If the resultant of force is not taken and directly use only the vertical component to calculate the solution then we will get option (C) , which will be wrong.